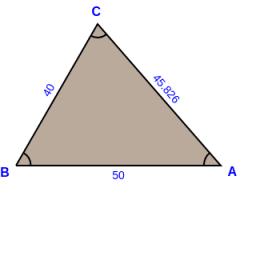
Souřadnice vrcholů
Vypočítejte souřadnice vrcholů trojúhelníku, pokud rovnice jeho stran jsou
7x-4y-1 = 0
x-2y + 7 = 0
2x + y + 4 = 0
Vaše odpověď:
7x-4y-1 = 0
x-2y + 7 = 0
2x + y + 4 = 0
Vaše odpověď:
Tipy na související online kalkulačky
Máte soustavu rovnic a hledáte kalkulačku soustavy lineárních rovnic?
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
geometriealgebraplanimetrieÚroveň náročnosti úkolu
Související a podobné příklady:
- Souřadnice bodu B
V trojúhelníku ABC určete souřadnice bodu B, pokud víte, že body A, B leží na přímce 3x-y-5=0, body A, C leží na přímce 2x+3y+4=0, bod C leží na souřadnicové ose x a úhel u vrcholu C je pravý. - Vrcholy trojúhelníku
Určete souřadnice vrcholu trojúhelníku ABC, známe-li středy SAB [0;3] SBC [1;6] SAC [4;5], jeho stran AB, BC, AC. - Určete 50
Určete souřadnice vrcholu obdélníku vepsaneho do kružnice x²+y² -2x-4y-20=0, vite-li, že jedna jeho strana leží na přímce p: x+2y=0 - Souřadnice vrcholů
Určete souřadnice vrcholů a obsah rovnoběžníku, jehož dvě strany leží na přímkách 8x + 3y + 1 = 0, 2x + y-1 = 0 a úhlopříčka na přímce 3x + 2y + 3 = 0 - Lichoběžník - strany
Velikost stran lichoběžníku jsou 3/4*x cm, x cm, 2*(x+1) cm a 3(x+2) cm. Pokud je jeho obvod 60 cm, vypočítejte délku každé strany. - Strany trojúhelníku
Vypočítejte strany trojúhelníku pokud S = 84 cm² a = x, b = x + 1, c = x + 2 - Těžiště
V trojúhelníku ABC leží bod D[1,-2,6], který je středem strany |BC| a bod G, který je těžištěm trojúhelníku G[8,1,-3]. Najděte souřadnice vrcholu A[x,y,z].
