Určete 4
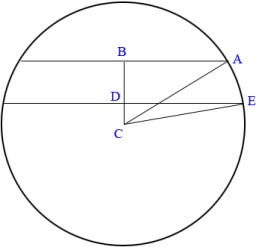
Určete vzdálenost dvou rovnoběžných tětiv délek 7 cm a 11 cm v kružnici s poloměrem 7 cm
Správná odpověď:
Tipy na související online kalkulačky
Chcete proměnit jednotku délky?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebraaritmetikaplanimetrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Vzdálenost rovnoběžných tětiv
Dvě rovnoběžné tětivy v kružnici o poloměru 6 cm mají délky 6 cm a 10 cm. Vypočítej jejich vzájemnou vzdálenost. Najdi obě řešení. - Tětiva 2
Bod A má od středu kružnice s poloměrem r = 5 cm vzdálenost 13 cm. Vypočítejte délku tětivy spojující body dotyku T1 a T2 tečen vedených z bodu A ke kružnici k. - Kružnice
V kružnici s poloměrem 7,5 cm jsou sestrojeny 2 rovnoběžné tětivy, jejichž délky jsou 9 cm a 12 cm. Vypočítejte vzdálenost těchto tětiv (pokud jsou možné dvě řešení napište obě). - Kružnice s dvěma tětivami
Dány jsou dvě úsečky různých délek. Sestrojte kružnici k tak, aby obě úsečky byly jejími tětivami. - Vzdálenost tětivy od středu
V kružnici o poloměru 10 cm je 12 cm dlouhá tětiva. Vypočítej vzdálenost tětivy od středu kružnice. - Tětiva - vzdálenost
V kružnici k (S; 6 cm) vypočítejte vzdálenost tětivy t od středu kružnice S, pokud délka tětivy je t = 10 cm. - Rovnoběžné tětivy
V kružnici s r = 26 cm jsou narýsované 2 rovnoběžné tětivy. Jedna tětiva má délku t1 = 48 cm a druhá má délku t2 = 20 cm, přičemž střed leží mezi nimi. Vypočítejte vzdálenost dvou tětiv.
