Náměstí 3

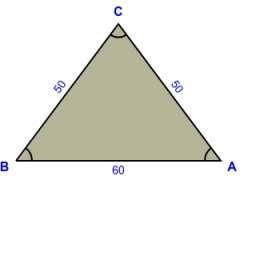
Vypočtěte rozlohu náměstí tvaru rovnoramenneho trojúhelníku s rameny 50 m a základnou 60 m. Kolik dlaždic se spotřebuje na vydlazdeni náměstí, jestliže plocha jedné dlaždice je 25 dm²?

Vaše odpověď:

Pomozte nám příklad zlepšit. Pokud jste našli chybu, dejte nám vědět. Děkujeme!

Tipy na související online kalkulačky

Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Chcete proměnit jednotku plochy?
Vypočet rovnoramenného trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.

K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:

algebra

úpravy výrazů

planimetrie

Pythagorova věta
pravoúhlý trojúhelník
obsah
trojúhelník

Jednotky fyzikálních veličin

převody jednotek
plocha

Úroveň náročnosti úkolu

8. ročník
9. ročník

Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1

Související a podobné příklady:

Dlaždice na chodník kolem bazénu
Obdélníkový bazén má rozměry 25 metrů a 12,5 metru. Kolem bazénu je stezka široká 2 metry. Kolik metrů čtverečních dlaždic je potřeba k vydláždění chodníku?
Spáry
Kolik dlaždic tvaru kosočtverce o straně 25 cm a výšce 20 cm je zapotřebí k vydláždění nádvoří tvaru obdélníku se stranami 30 m a 28 m, jestliže spáry představují 1/20 plochy?
Náklady
Náklady na vydláždění podlahy o rozměrech 7 x 6 čtverečních stop jsou 2 100 USD. Kolik bude stát dlaždice na podlaze o rozměrech 11 x 13 čtverečních stop?
Dlaždice 2
Kolik čtvercových dlaždic o obsahu 121 cm² se musí objednat pro vydláždění čtvercové místnosti o straně délky 2,75 m?
Štít domu
Vypočítejte výšku štítu domu, který má tvar rovnoramenného trojúhelníku se základnou 8,4 m a rameny 6,5 m.
Rozměry dlaždic
Kolik dlaždic je potřeba na pokrytí podlahy koupelny, která má tvar obdélníku o rozměrech 4 m a 25 dm. Dlaždice jsou tvaru čtverce s rozměry 10 cm.
Počet květin na záhon
Květinový záhon má tvar rovnoraměného trojúhelníku se základnou 25 m a rameny 30 m dlouhými. Vypočítej, nejvíc kolik květin můžeme na tento záhon vysadit, pokud předpokládáme, že jeden květ potřebuje asi 8 dm čtverečních plochy. Výsledek zaokrouhlí na des