Kůlna
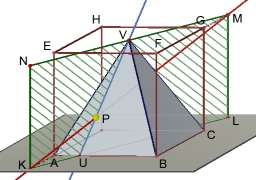
Kůlna tvaru kvádru je kryta střechou tvaru čtyřbokého jehlanu s podstavou o hranách 6 m a 3 m a výškou 2,5 m. Kolik m2 (metrů čtverečních) je třeba zakoupit, jestliže na překrytí krytiny a odpad se počítá 40% navíc?
Vaše odpověď:
Vaše odpověď:
Tipy na související online kalkulačky
Naše kalkulačka pro výpočet procent Vám pomůže rychle vypočítat různé typické úlohy s procenty.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
aritmetikastereometrieplanimetriezákladní operace a pojmyJednotky fyzikálních veličinÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Rozhledna 4
Rozhledna je kryta střechou tvaru pravidelného čtyřbokého jehlanu s podstavnou hranou 8 m a výškou 6 m. 60% krytiny je třeba vyměnit. Kolik m² je třeba zakoupit? - Autobusová
Autobusová čekárna má tvar pravidelného čtyřbokého jehlanu vysokého 4 m s hranou podstavy o velikosti 5 m. Vypočítejte, kolik m² střešní krytiny je třeba na pokrytí tří stěn pláště, bereme-li v úvahu 40% krytiny navíc na překrytí. - Plocha plechu na věž
Věž má tvar pravidelného čtyřbokého jehlanu s podstavou hranou 0,8 m. Výška věže je 1,2 metru. Kolik metrů čtverečních plechu je třeba na pokrytí počítáme-li osm procent na spoje a překrytí? - Střecha
Střecha má tvar pláště rotačního kuželu s průměrem podstavy 6 m a výškou 2,5 m. Kolik korun bude stát plech na pokrytí střechy, jestliže 1 m² plechu stojí 152 Kč a jestliže na spoje, překrytí a odpad je nutné zakoupit 15% navíc? - Zámecká věž
Zámecká věž má střechu kuželu s průměrem 10 metrů a výškou 8 metrů. Vypočítejte, kolik m² krytiny je třeba na její pokrytí, uvažujeme-li navíc jednu třetinu na překrytî. - Věž
Kolik metrů čtverečních je potřeba na pokrytí věže tvaru pravidelného čtyřbokého jehlanu o podstavné hraně 10 metrů, je-li odchylka boční hrany od roviny podstavy 68°? Při pokrytí se počítá s odpadem 10%. - Střešní krytina jehlanu
Střecha domu má tvar pravidelného čtyřbokého jehlanu vysokého 4 m s hranou podstavy o velikosti 100 dm. Vypočítejte, kolik m² střešní krytiny je zapotřebí k pokrytí střechy, pokud bereme v úvahu 30% krytiny navíc k překrytí.
