Kružnice
Najděte rovnice kružnic, které procházejí body A (-2; 4) a B (0, 2) a dotýkají se osy x.
Vaše odpověď:
Vaše odpověď:
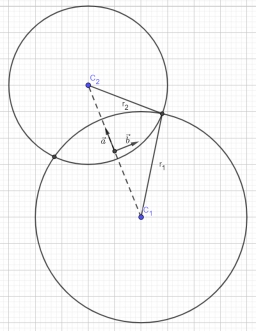
Tipy na související online kalkulačky
Hledáte pomoc s výpočtem kořenů kvadratické rovnice?
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
geometriealgebraplanimetrieÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Lichoběžník - souměrnost
Najděte k bodům A[-4,0], B[-1,4] body A1, B1 souměrné podle osy y. Vypočítejte obvod lichoběžníku AB B1 A1. - Setrvačník
Setrvačník koná 450 ot/min. Určete velikost normálového zrychlení bodů setrvačníku, které jsou ve vzdálenosti 10 cm od osy otáčení. - Rovnice kružnice
Najděte rovnici kružnice, která se dotýká osy y ve vzdálenosti 4 od počátku a vysekne tětivu délky 6 na ose x. - Rovnice kružnice
Najděte rovnici kružnice, jejíž průměr má koncové body (1,-4) a (3,2). - Vzdálenost středů dotýkajících se kružnic
Kružnice s poloměry r1=10 centimetrů a r2=4 cm se zvenčí dotýkají. Jaká je vzdálenost jejich středů? - Rovnice elipsy body A, B
Napište rovnici elipsy, která prochází body a její osy jsou totožné se souřadnicovými osami, když: A = [2, 3] a B = [−1, −4]. - Koule
Najděte rovnici koule pokud na povrchu koule leží tři body (a, 0,0), (0, a, 0), (0,0, a) a střed leží na rovině x + y + z = a.
