Geometrie - příklady - strana 2 z 37
Počet nalezených příkladů: 735
- Souřadnice průsečíků
 Jaký je součet všech souřadnic bodů, které jsou průsečíky přímky p: x = -1-2t, y = 5-4t, z = -3+6t, kde t je reálné číslo, se souřadnicovými rovinami xy a yz?
Jaký je součet všech souřadnic bodů, které jsou průsečíky přímky p: x = -1-2t, y = 5-4t, z = -3+6t, kde t je reálné číslo, se souřadnicovými rovinami xy a yz? - Kolmá a rovnoběžná
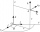 Potřebuji matematickou pomoc v tomto problému: jsou dány dva trojrozměrné vektory a = (- 5, 5 3) b = (- 2, -4, -5) Rozložte vektor b na b = v + w, kde v je rovnoběžná s a a w je kolmá na a. Najděte souřadnice vektorů v a w.
Potřebuji matematickou pomoc v tomto problému: jsou dány dva trojrozměrné vektory a = (- 5, 5 3) b = (- 2, -4, -5) Rozložte vektor b na b = v + w, kde v je rovnoběžná s a a w je kolmá na a. Najděte souřadnice vektorů v a w. - CVD=52°30minut 32011
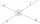 Vypočítej velikost úhlu BVC, pokud pro velikosti úhlů platí: AVB=37°48minut, CVD=52°30minut, AVD=118°
Vypočítej velikost úhlu BVC, pokud pro velikosti úhlů platí: AVB=37°48minut, CVD=52°30minut, AVD=118° - Smernicový tvar
 Najděte rovnici přímky procházející bodem A [9, -3] a sklonem - směrnicí -1,4. Odpověď zapište ve tvaru y = ax + b, kde a, b jsou konstanty.
Najděte rovnici přímky procházející bodem A [9, -3] a sklonem - směrnicí -1,4. Odpověď zapište ve tvaru y = ax + b, kde a, b jsou konstanty. - Koeficienty rovnice
 Jaká je rovnice přímky, jejíž průsečík x je -3 a průsečík y je -4? Najděte koeficienty A, B, C v normálové rovnici přímky: Ax + By = C
Jaká je rovnice přímky, jejíž průsečík x je -3 a průsečík y je -4? Najděte koeficienty A, B, C v normálové rovnici přímky: Ax + By = C - Parametrické vyjádření
 Bod A [6; -2]. Bod B = [-3; 1] Zapiš parametrické vyjádření úsečky BA tak, aby t patřilo do uzavřený interval < 0;3 >
Bod A [6; -2]. Bod B = [-3; 1] Zapiš parametrické vyjádření úsečky BA tak, aby t patřilo do uzavřený interval < 0;3 > - Procházela 11311
 Čára procházela třemi body - viz tabulka: x y -6 4 -4 3 -2 2 Napište přímkovou rovnici ve tvaru y=mx+b.
Čára procházela třemi body - viz tabulka: x y -6 4 -4 3 -2 2 Napište přímkovou rovnici ve tvaru y=mx+b. - Pět řešení
 Urči pět řešení rovnice o dvou neznámých. Zapiš jako uspořádané dvojice a zakresli do grafu. Jak vypadá graf lineární rovnice? 2x+3y=7
Urči pět řešení rovnice o dvou neznámých. Zapiš jako uspořádané dvojice a zakresli do grafu. Jak vypadá graf lineární rovnice? 2x+3y=7 - Číselnou 53581
 Bod P je na úsečce OQ. Pokud je OP = 6, OQ = 4x - 3 a PQ = 3x, najděte číselnou délku úsečky OQ.
Bod P je na úsečce OQ. Pokud je OP = 6, OQ = 4x - 3 a PQ = 3x, najděte číselnou délku úsečky OQ. - Přímka
 Napište rovnici přímky rovnoběžné s 9x + 3y = 8, která prochází bodem (-1, -4). Napište ve tvaru ax + by = c.
Napište rovnici přímky rovnoběžné s 9x + 3y = 8, která prochází bodem (-1, -4). Napište ve tvaru ax + by = c. - Najděte
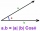 Najděte vektor v4 kolmý na vektory v1 = (1, 1, 1, -1), v2 = (1, 1, -1, 1) a v3 = (0, 0, 1, 1)
Najděte vektor v4 kolmý na vektory v1 = (1, 1, 1, -1), v2 = (1, 1, -1, 1) a v3 = (0, 0, 1, 1) - Sousední úhly
 Jeden ze sousedních úhlů je větší než druhý o 33°. Vypočtěte velikost úhlů.
Jeden ze sousedních úhlů je větší než druhý o 33°. Vypočtěte velikost úhlů. - Kolmice
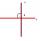 Určitě směrnici přímky kolmé na přímku p: y = 7x -3.
Určitě směrnici přímky kolmé na přímku p: y = 7x -3. - Určete 3
 Určete průsečík dvou přímek p a q je-li. : p:3y+2x-5=0 q:4x+7y-11=0
Určete průsečík dvou přímek p a q je-li. : p:3y+2x-5=0 q:4x+7y-11=0 - Nakreslite
 Nakreslite graf funkcie y = -2x + 3 a vyrátajte súradnice priesečníkov grafu funkcie s osami x a y
Nakreslite graf funkcie y = -2x + 3 a vyrátajte súradnice priesečníkov grafu funkcie s osami x a y - Kolmé 3D vektory
 Najděte vektor a = (2, y, z) tak, že a⊥b a ⊥ c kde b = (-1, 4, 2) a c = (3, -3, -1)
Najděte vektor a = (2, y, z) tak, že a⊥b a ⊥ c kde b = (-1, 4, 2) a c = (3, -3, -1) - Sousední úhly
 Jeden ze sousedních úhlů je 3 krát větší než druhý. Jakou má velikost větší ze sousedních úhlů?
Jeden ze sousedních úhlů je 3 krát větší než druhý. Jakou má velikost větší ze sousedních úhlů? - Lichoběžník - čtyri strany
 lichoběžník- 40,5+42,5+52,8+35,0. Vypočti obsah
lichoběžník- 40,5+42,5+52,8+35,0. Vypočti obsah - MIT 1869
 Znáte délku částí 9 a 16, na které přeponu pravoúhlého trojúhelníku rozdělí kolmice spuštěná z jeho protilehlého vrcholu. Úkolem je zjistit délky stran trojúhelníku a délku úsečky x. Tato úloha byla součástí přijímacích zkoušek na Massachusettský technolo
Znáte délku částí 9 a 16, na které přeponu pravoúhlého trojúhelníku rozdělí kolmice spuštěná z jeho protilehlého vrcholu. Úkolem je zjistit délky stran trojúhelníku a délku úsečky x. Tato úloha byla součástí přijímacích zkoušek na Massachusettský technolo - Trojúhelníky podobné
 Trojúhelníky ABC a A'B'C'. Jsou podobné. V trojúhelníku ABC jsou velikosti dvou úhlů 25 stupňů a 65 stupňů. Zdůvodni proč v trojúhelníku A'B'C' je součet velikosti dvou úhlů roven 90 stupňů.
Trojúhelníky ABC a A'B'C'. Jsou podobné. V trojúhelníku ABC jsou velikosti dvou úhlů 25 stupňů a 65 stupňů. Zdůvodni proč v trojúhelníku A'B'C' je součet velikosti dvou úhlů roven 90 stupňů.
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
