Kombinatorika - slovní úlohy a příklady - strana 17 z 53
Počet nalezených příkladů: 1044
- Na salame
Kolika způsoby mohu vybrat 5ks salámů, přičemž mám k dispozici 6 druhů salámů po 10 kusech a jeden druh se 4 kusy? - Trojúhelník - kombinace
Zjisti kolik trojúhelníků vytvoříš z úseček o délkách 7 dm, 5 dm, 10 dm, 12 dm, 15 dm. - Logik
Písmenkový Logik je hra pro dva hráče, která má následující pravidla: 1. První hráč si myslí pětipísmenné slovo, v němž se žádné písmeno ne- opakuje. 2. Druhý hráč napíše nějaké pětipísmenné slovo. 3. První hráč odpoví dvěma čísly — první číslo udává, kol - Nezávislý člen
Najděte člen nezávislý na x v roznásobeném zápisu polynomu (4x³+1/2x)8 - N-úhelník
Kolik vnitřních úhlopříček má konvexní 10-úhelník? - Dělitele
Kolik různých dělitelů má číslo 2 5 * 17 6? - Šachy
Kolika možnými způsoby se dá zahájit šachová partie (první tah)? - Pravděpodobnost 17013
Jaká je pravděpodobnost, že náhodně napsané dvouciferné číslo od číslo 20 do čísla 99 bude nebo je dělitelné 11, nebo mocnice čísla 3, nebo prvočíslo? - Nejrychlejší 5508
Na závod Akčesou přijelo 25 běžců. Běžecká dráha byla však úzká a proto mohli běžet vždy jen pět běžci najednou. Co však překvapilo Sáru s Arthurem nejvíc, byl fakt, že Te-TiVáci nemají stopky a ani jiné přístroje, kterými by běžcům uměli přesně změřit je - Z klobouku
Při losování čísel z klobouku od 1 do 35 vybíráme náhodné dané čísla. Jaká je pravděpodobnost že vylosované čísla budou dělitelné 8 a 2? - Elektrický obvod
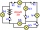Zde máš úkol tak trochu k přemýšlení, ale velkou složitost v tom nehledej. Máš tu zapojeno 6 žárovek A až F a 6 spínačů č. 1 až č. 6. Tvým úkolem bude postupně určit, které žárovky budou vždy svítit, pokud bude některý ze spínačů v poloze vypnuto - Vlastnosti: 15511
Věc, do které vhodíte peněz a umíte se přes ni pak dívat jako přes dalekohled, má v sobě celou sadu 81setových kartiček. Kolik existuje platných setů, které obsahují alespoň jednu modrou kartičku? Sety jsou karetní hra. Každá setová karta má 4 vlastnosti: - Dvojčata
Jak víte, na začátku školního roku jezdí noví studenti na adaptační kurzy. V jedné třídě se rozdělili na dvě nestejně velké skupinky. Větší se rozhodla hrát fotbal, menší měla v plánu hrát basketbal. Jenže právě u té menší skupinky se objevil nečekaný pro - Cyklostezka 39643
Ze Zubrohlavy do Bobrova vede jedna asfaltová cesta, dvě lesní cesty a jedna cyklostezka. Určete počet způsobů, kterými se dostaneme ze Zubrohlavy do Bobrova a zpět. Vypište všechny možnosti. - Postavit 64304
Kolika různými způsoby se mohou postavit do řady v jídelně Anka, Betka, Cyril, Daniel a Erik, pokud kluci pustí obě dívky před sebe? - Ciferných 42291
Kolik existuje 5 ciferných lichých čísel? - Olympiáda
Kolika způsoby se mohou umístit 6 závodníci na medailových pozicích na olympiádě? Na barvě kovu záleží. - KLADIVO 3
Určete, kolika způsoby lze přemístit písmena slova KLADIVO tak, aby v tomto přemístění nějaká skupina po sobě jdoucích písmen tvořila slovo VODA. - Majitel firmy
Majitel firmy s rozsáhlou administrativní činností chce svým zaměstnancům odprodat 3 zastaralé stroje v ceně 1000 kč za 1 stroj a s půlroční záruční lhůtou. Jestliže se stroj v této době porouchá, majitel vrátí zaměstnanci peníze a navíc ještě vydá 100 kč - Tréninky
V tabulce je harmonogram sobotních tenisových tréninků mladších žáků během zimní halové sezóny. Před začátkem letní sezóny se připravuje nový harmonogram tréninků. Tomáš Kučera bude moci trénovat jen dopoledne, sestry Kováčová budou muset trénovat v libov
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám tenhle příklad a my Ti ho zkusíme vypočítat.
