Příklady na pravoúhlý trojúhelník - strana 31 z 84
Počet nalezených příkladů: 1667
- Zkratka
Představte si, že jdete ke kamarádovi po rovné cestě. Ta cesta má délku 350 metrů. Potom zahnete doprava a půjdete dalších 1790 metrů a jste u kamaráda. Otázka zní, o kolik bude kratší cesta, když půjdete přímou cestou přes pole? - V rovnoramenném trojúhelníku
V rovnoramenném trojúhelníku ABC se základnou AB; A [-3,4]; B [1,6] leží vrchol C na přímce 5x - 6y - 16 = 0. Vypočítejte souřadnice vrcholu C. - Úloha o pohybu
Z křižovatky dvou kolmých silnic vyjeli současně dva cyklisté (každý jinou silnicí) jeden jede průměrnou rychlostí 16 km/h, druhý průměrnou rychlostí 24 km/h. Určete jejich vzájemnou vzdálenost po 25 minutách jízdy. - Odvěsna a výška
Řešte pravoúhlý trojúhelník, je-li dána jeho výška v = 8,5 m a kratší odvěsna b = 15,7 m.
- MIT 1869
Znáte délku částí 9 a 16, na které přeponu pravoúhlého trojúhelníku rozdělí kolmice spuštěná z jeho protilehlého vrcholu. Úkolem je zjistit délky stran trojúhelníku a délku úsečky x. Tato úloha byla součástí přijímacích zkoušek na Massachusettský technolo - MO Z9 2019 domace kolo
V trojúhelníku ABC leží bod P ve třetině úsečky AB blíže bodu A, bod R je ve třetině úsečky P B blíže bodu P a bod Q leží na úsečce BC tak, že úhly P CB a RQB jsou shodné. Určete poměr obsahů trojúhelníků ABC a PQC. - Součet obsahů
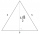Nád výškou rovnostranného trojúhelníku ABC je sestrojen rovnostranný trojúhelník A1, B1, C1, nad jeho výškou je sestrojen rovnostranný trojúhelník A2, B2, C2, atd. Se postup neustále opakuje. Jaký je velký součet obsahů všech trojúhelníků, pokud strana tr - Ethernet cez ulici
Karel a Jirka jsou vášniví hráči počítačových her a bydlí v domech, které jsou přesně naproti sobě přes ulici, takže si vidí navzájem do oken. Rozhodli se, že si své počítače propojí telefonním kabelem aby mohli hrát společně hry. Karel bydlí v prvním pat - Úhel stoupání
Velikost úhlu stoupání přímé cesty je přibližně 12 °. Určete stoupání této cesty v procentech.
- Tři kamarádi 8
Tři kamarádi sedí na molu, které je přesně uprostřed tekoucí řeky. prvni kamarád se vydává proti proudu řeky rychlostí 0,4 m/s, druhý kamarád se vydává po proudu řeky rychlostí 0,2 m/s, třetí kamarád pluje kolmo směrem ke břehu rychlostí 0,8 m/s. Rychlost - Bombardér
Z jaké vzdálenosti před cílem musí být z letadla letícího ve výšce 1260 m shozen náklad na padáku, jestliže se snáší rychlostí 5,6 m/s a současně je unášen ve směru pohybu rychlostí 12 m/s. Jaká je přímá vzdálenost letadla od cíle? (Nejdříve si vypočítejt - Plavec 2
Plavec plave vzhledem k vodě stálou rychlostí 0,85 m/s. Rychlost proudu v řece je 0,40 m/s, šířka řeky je 90 m. a) Jak velká je výsledná rychlost plavce vzhledem ku stromu na břehu řeky, pohybuje-li se kolmo k proudu? b) Za jakou dobu plavec přeplave řeku - Gimli Glider
Letadlu Boeing 767 vypadly ve výši 35000 feet oba motory. Letadlo udržuje kapitán v optimálním klouzavém létě. Každou minutu však ztratí 2000 feet výšky a pilot udržuje konstantní rychlost 196 knots. Vypočítejte kolik bude trvat let od vysazení motorů po - Vektory v prostoru
Dáno jsou vektory u = (1; 3; -4), v = (0; 1; 1). Určete velikost těchto vektorů, Vypočtěte úhel vektorů, vzdálenost mezi vektory.
- Stoupání v procentech
Výškový rozdíl mezi místy A, B je 421 m. Vypočítejte procento stoupání cesty, když vodorovná vzdálenost míst A, B je 9,2 km. - Hloubkový úhel
Z pozorovací věže ve výšce 105 m nad hladinou moře je zaměřena loď v hloubkovém úhlu 1°49´. Jak daleko je loď od paty věže? - MO Z7–I–6 2021
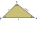V trojúhelníku ABC leží na straně AC bod D a na straně BC bod E. Velikosti úhlů ABD, BAE, CAE a CBD jsou postupně 30°, 60°, 20° a 30°. určete velikost úhlu AED. - Z9 – I – 2 MO 2018
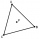V rovnostranném trojúhelníku ABC je K středem strany AB, bod L leží v třetině strany BC blíže bodu C a bod M leží v třetině strany AC blíže bodu A. Určete, jakou část obsahu trojúhelníku ABC zabírá trojúhelník KLM. - Z8-I-2 MO 2017
V ostroúhlém trojúhelníku KLM má úhel KLM velikost 68°. Bod V je průsečíkem výšek a P je patou výšky na stranu LM. Osa úhlu P V M je rovnoběžná se stranou KM. Porovnejte velikosti úhlů MKL a LMK.
Na cestě je značka pro stoupání s úhlem 7%. Vypočtěte pod jakým úhlem (v stupních) cesta stoupá (klesá).Máš příklad, nad kterým si přemýšlíš alespoň 10 minut? Pošli nám příklad a my Ti ho zkusíme vypočítat.
