Pythagorova věta - slovní úlohy a příklady - strana 47 z 72
Počet nalezených příkladů: 1439
- Krychle
Krychle je vepsána do koule o objemu 1579 cm³. Určete délku hrany krychle. - Kužel s průměrem
Nádoba tvaru kužele s průměrem dna 60cm a boční stranou délky 0,5m je zcela naplněna vodou. Vodu přelijeme do nádoby, která má tvář válce o poloměru 3dm a výšce 20cm. Bude válec přetékat, nebo naopak nebude plný? Vypočítejte kolik vody přeteče, nebo naopa - Iglu stan
Stan ve tvaru kužele je vysoký 3 m, průměr jeho podstavy je 3,2 m. a) Stan je vyroben je ze dvou vrstev materiálu. Kolik m² látky třeba na výrobu (včetně podlahy), pokud k minimálnímu množství třeba kvůli odpadu při stříhání přidat 20%? b) Kolik m³ vzduch - Pyramidy v Gize
Petr si z dovolene v Egypte přivezl model pyramidy ve tvaru pravidelného čtyřbokého jehlanu. Změřil si že jeji podstavna hrana má delku 7cm a bočni hrana má delku 10 cm. Model má hmotnost 1kg a je vyroben z neznámého kovu. Z jakeho kovu je model vyroben? - Drátěný model
Drátěný model pravidelného šestibokého hranolu s podstavnou hranou délky a = 8 cm má výšku v = 12 cm. Těleso se přelepí papírem, podstavy tmavým a plášť bílým. - Vypočtěte v cm největší možnou přímou vzdálenost dvou vrcholů drátěného hranolu (tloušťku drá - Těžiště tetraeder
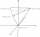Určete polohu těžiště soustavy čtyř hmotných bodů, které mají hmotnosti, m1, m2 = 2m1, m3 = 3M1 a m4 = 4m1, pokud leží ve vrcholech rovnoramenné tetraedru. (Ve všech případech mezi sousedními hmotnými body je vz - Rovnostranny kužel
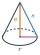Do nádoby tvaru rovnostranného kužele, jehož podstava má poloměr r = 6 cm nalijeme tolik vody, že se naplní jedna třetina objemu kužele. Do jaké výšky bude sahat voda, pokud kužel obrátíme dnem vzhůru? - Neštěstí
Pana Radomíra při poslední bouřce postihlo neštěstí, na střechu tvaru pravidelného čtyřbokého jehlanu mu spadl strom a celou mu ji poničil. Střecha má podstavou délku hrany 8m a délku boční hrany 15m. Kolik m² střešní krytiny bude muset nakoupit? - Válec
Válec je třikrát vyšší než je jeho šířka. Délka úhlopříčky válce je 20 cm. Najděte plochu horní části válce. - Dopravní kužely
Čtyřicet stejných dopravních kuželů s průměrem podstavy d=3dm a výškou v=6dm máme natřít zvenčí oranžovou barvou (bez podstavy). Kolik korun zaplatíme za barvu, pokud na natření 1m² potřebujeme 50 cm³ barvy a 1l barvy stojí 80 Kč? - Jáma
Jáma ve tvaru komolého jehlanu s obdélníkovými podstavami a je hluboká 3,1 m. Délka a šířka jámy je navrchu 3 × 1,5 m, dole 1 m × 0,5 m. Na natření 1 metre čtvereční jámy je třeba 1,4 l zelené barvy. Kolik litrů barvy se na její natření použije, pokud nat - Plovák
0,5 m kulovitý plovák je používán jako umístění ochranné značky pro kotvící rybářské lodě. Plave ve slané vodě. Najděte hloubku, ve které plovák klesá v případě, že materiál, ze kterého je vyroben váží 8 kilogramů na metr krychlový a slaná voda hmotnost 1 - Součet velikostí hran
Vypočtěte povrch kvádru, je-li dán součet velikostí jeho hran a+b+c=19 cm a velikost tělesové úhlopříčky u=13 cm. - Jehlan
Urči povrch pravidelného čtyřbokého jehlanu, když je dán jeho objem V = 120 a úhel boční stěny s rovinou podstavy je α = 42° 30'. - Plovoucí sud
Na vodě plave sud tvaru válce, a to tak že z vody vyčnívá 18 dm do výšky a na hladině má šířku 33 dm. Délka sudu je 20 dm. Vypočítejte objem sudu. - Autobusová
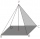Autobusová čekárna má tvar pravidelného čtyřbokého jehlanu vysokého 4 m s hranou podstavy o velikosti 5 m. Vypočítejte, kolik m² střešní krytiny je třeba na pokrytí tří stěn pláště, bereme-li v úvahu 40% krytiny navíc na překrytí. - Stan pro skauty
Stan pro skauty má dřevěnou obdélníkovou podsadu s rozměry 220 cm a 150 cm. Kolik plátna je třeba na střechu tvaru čtyřbokého jehlanu vysokého 170 cm? - Stříška
Pan Peter má nad studní plechovou stříšku tvaru kužele o výšce 101 cm a poloměru 189 cm. Stříška potřebuje natřít antikorozní barvou. Kolik kg barvy musí nakoupit, jestliže výrobce udává spotřebu 1kg na 4,3 m²? - Stan
Stan tvaru pravidelného čtyřbokého jehlanu má délku podstavné hrany a=2m a výšku v=1,8m. Kolik m² plátna potřebujeme na ušití stanu, musíme-li přidat 7% na švy? Kolik m³ bude ve stanu? - Střecha Nad pavilonem se čtvercovým půdorysem se stranou délky a = 12 m je střecha tvaru pláště jehlanu s výškou v = 4,5 m. Vypočítejte, kolik m² plechu třeba k zakrytí této střechy, jestliže na spoje a odpad třeba počítat 5,5% plechu.
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám tenhle příklad a my Ti ho zkusíme vypočítat.
