Pythagorova věta - slovní úlohy a příklady - strana 46 z 72
Počet nalezených příkladů: 1439
- Trojboký jehlan
Vypočítejte objem a povrch pravidelného trojbokého jehlanu, jehož výška je stejná jako délka hrany podstavy 10 cm. - Dvě koule
Dvě koule, jedna s poloměrem 8 cm a další s poloměrem 6 cm, se vloži do válcové plastové nádoby s poloměrem 10 cm. Najděte množství vody potřebné k jejich potopení. - Komolý jehlan
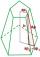Vypočtěte objem pravidelného šestibokého komolého jehlanu, jestliže je délka hrany dolní podstavy 30 cm, horní podstavy 12 cm a pokud délka boční hrany je 41 cm. - Petra 4
Petra má ve dvou bedničkách tvaru krychle zasazené květiny. První bednička má vnitřní rozměr 70 cm a druhá 5dm. Chce si vyrobit jednu bedničku tvaru kvádru, kam by obě květiny z těchto bedniček přesadila. Nová bednička má mít stejný vnitřní objem jako obě - 4-boký jehlan v2
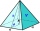Vypočítejte objem a povrch pravidelného čtyřbokého jehlanu, jeli obsah podstavy 20 cm². Odchylka boční hrany od roviny podstavy je 60 stupňů. - Kvádr težší
Kvádr má objem 32 cm³. Jeho plášť má dvojnásobný obsah než jedna ze čtvercových podstav. Jakou délku má tělesová úhlopříčka? - Úhlopříčkou 3
Úhlopříčkou řezu DBFH pravidelného čtyřbokého hranolu ABCDEFGH je vepsán kruh o průměru 8 cm. Jaký je objem hranolu. - Vrchol 9
Vrchol věže má tvar pravidelného šestibokého jehlanu. Podstavná hrana má délku 1,2 m, výška jehlanu je 1,6 m. Kolik metrů čtverečných plechu je potřeba na pokrytí vrcholu věže, je-li na spoje, překrytí a odpad zapotřebí 15% plechu navíc? - Kvádr
Kvádr s hranou a=7 cm a tělesových úhlopříčkou u=33 cm má objem V=3136 cm³. Vypočítejte velikosti ostatních hran. - Karnevalova čepice
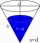Kolik dm² ozdobného papíru je potřeba ke zhotovení karnevalových čepic tvaru kužele pro 46 prvňáků, pokud obvod hlavy prvňáčka je 49 cm a výška čepice má být 33 cm. Na záhyby je nutné přidat 3% papíru? - Kužel
Vypočítej objem a povrch kužele, pokud průměr podstavy je d = 14 cm a strana kužele svírá s rovinou podstavy úhel 34°24'. - Věžička 2
Věžička má půdorys tvaru čtverce s délkou strany 5m. Střecha věžičky má tvar pravidelného čtyřbokého jehlanu (bez podstavy) s výškou 8m. Při rekonstrukci se bude střecha pokrývat novými taškami. Na 1 m² se spotřebuje 11 tašek. Na jedné paletě je uskladněn - Dřevená 3
Dřevená deska dlouhá 2,5m má pruřez tvaru pravidelného lichobežníku jehož rovnobežné strany májí delku 1,2dm a 8cm vyška lichobežníka je 3cm. Vypočtete: a) povrch desky pro vypočet spotřeby mořidla b) hmotnost desky je-li hustota dřeva je 600kg/m³ c) koli - Věžička Věžička má tvar pravidelného čtyřbokého jehlanu s podstavnou hranou délky 0,8 m. Výška věžičky je 1,2 m. Kolik metrů čtverečných je potřeba na její pokrytí, počítáne-li na odpad 10% plechu navíc.
- Kvádr 68
Kvádr má tělesovou úhlopříčku u=25 cm a strana b je oproti straně a o třetinu delší. Jaký je objem kvádru? - Na louce
Na louce přistála kosmická loď ve tvaru koule o průměru 6 m. Aby nepoutala pozornost, zakryli ji marťanci střechou ve tvaru pravidelného kužele. Jak vysoká bude tato střecha, aby spotřeba krytiny byla minimální? - Tajný poklad
Skauti mají stan ve tvaru pravidelného čtyřbokého jehlanu se stranou podstavy 4 m a výšce 3 m. Do stanu potřebují schovat válcovou nádobu s tajným pokladem. Určete poloměr r (a výšku h) nádoby tak, aby mohli schovat co nejobjemnější poklad. - Kulečník
Vrstva slonovinových kulečníkových koulí o poloměru 6,35 cm, je ve tvaru čtverce. Koule jsou uspořádány tak, že každá koule je tangenty (dotýká se) každé sousedící s ní. V prostorech mezi 4 přilehlými koulemi je prostor rovný velikosti originálu kouli. Po - Čtyrstěn
Vypočtěte výšku a objem pravidelného čtyřstěnu, jehož hrana má délku 13 cm. - Kužel S2V
Plášť kužele rozvinutý do roviny má tvar kruhové výseče se středovým úhlem 126° a obsahem 415 cm². Vypočítejte objem tohoto kužele.
Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
