Pythagorova věta + čtyřúhelník - příklady a úlohy
Počet nalezených příkladů: 29
- Obsah
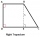
Vypočítejte obsah čtyřúhelníku, jehož dvě a dvě strany jsou stejně dlouhé a rovnoběžné o délkách stran 11, 5, 11 a 5. Vnitřní úhly čtyřúhelníku jsou 45°, 135°,45°, 135°. - Čtyřúhelník
Urč o jaký čtyřúhelník ABCD jde a vypočítej jeho obvod A/2,4/, B/-2,1/, C/-2,-2/, D/2,-5/. A. Útvar je: B. Jeho obvod měří: - Čtyřúhelníku 80729
Čtyřúhelník ABCD má délky stran AB=13cm, CD=3cm, AD=4cm. Úhly ACB a ADC jsou pravé. Vypočítej obvod čtyřúhelníku ABCD. - PQ=4*vektor 78264
PQRS je čtyřúhelník s P(4,4), S(8,8) a R(12,8). Pokud vektor PQ=4*vektor SR, najděte souřadnice Q. Vyřešte to - Čtyřúhelník
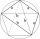Čtyřúhelník ABCD je složen ze dvou pravoúhlých trojúhelníků ABD a BCD. Pro délky stran platí: | AD | = 3cm, | BC | = 12cm, | BD | = 5cm. Kolik centimetrů čtverečních má čtyřúhelník ABCD? Úhly DAB a DBC jsou pravé. - Čtyřúhelníku 54791
Sestroj trojúhelník ABC pokud c=5cm, b=7cm a a=4cm. Potom vytvoř rovnoběžník, osově souměrný s úsečkou AC a změř velikost druhé úhlopříčky tohoto čtyřúhelníku. - Nepravidelný čtyřúhelník
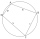Daný je 4-úhelník ABCD vepsaný do kružnice, přičemž úhlopříčka AC je průměr kružnice. Vzdálenost bodu B od průměru je 15 cm, vzdálenost bodu D od průměru je 18 cm. Vypočítejte poloměr kružnice a obvod 4-úhelníku ABCD.
- Čtyřúhelník
Ukažte, že čtyřúhelník s vrcholy P1 (0,1), P2 (4,2) P3 (3,6) P4 (-5,4) má dva pravé trojúhelníky. - Nepravidelný čtyřúhelník
Vypočítej velikost strany d = |AD| ve čtyřúhelníku ABCD: a= 35m, b= 120m, c=85m, úhel ABC = 105 stupňů, úhel BCD= 72 stupňů - Tunel - čtyřúhelník
Jak dlouhý bude tunel AB, vzdálenosti AD=35 m, DC=120 m, CB=85 ma úhly ADC=105 stupňů a BCD=71 stupňů. ABCD je čtyřúhelník. - Rovnostranný 81097
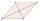Čtyřúhelník ABCD je souměrný podle úhlopříčky AC. Délka AC je 12 cm, délka BC je 6 cm a vnitřní úhel u vrcholu B je pravý. na stranách AB, AD jsou dány body E, F tak, že trojúhelník ECF je rovnostranný. Určete délku úsečky EF. - Výslednice 3
Na hmotný bod působí dvě stejné síly o velikosti 30 N. Urči velikost výslednice, svírají-li tyto síly úhel 42°. - Nepřístupne místa
Určete vzdálenost dvou nepřístupných míst P, Q, pokud vzdálenost dvou pozorovacích míst A, B je 2000m a znáte-li velikost úhlů QAB = 52°40'; PBA = 42°01'; PAB = 86°40' a QBA = 81°15'. Uvažovaná místa A, B, P, Q leží v jedné rovině. - 4-boký jehlan v2
Vypočítejte objem a povrch pravidelného čtyřbokého jehlanu, jeli obsah podstavy 20 cm². Odchylka boční hrany od roviny podstavy je 60 stupňů. - Kosý hranol
Jaký objem má čtyřboký kosý hranol s podstavnými hranami o délce a=1m, b=1,1m, c=1,2m, d=0,7m, jestliže boční hrana o délce h=3,9m má odchylku od podstavy 20°35´ a hrany a, b svírají úhel 50,5°.
- Čtyřboký jehlan
Jaký je povrch pravidelného čtyřbokého jehlanu, když je podstavná hrana a=16 a výška v=19? - V pravidelném 2
V pravidelném čtyřbokem jehlanu je výška 6,5 cm a úhel mezi podstavou a boční stěnou je 42°. Vypočítej povrch a objem tělesa. Výpočty zaokrouhlit na 1 desetinné místo. - Věž
Kolik metrů čtverečních je potřeba na pokrytí věže tvaru pravidelného čtyřbokého jehlanu o podstavné hraně 10 metrů, je-li odchylka boční hrany od roviny podstavy 68°? Při pokrytí se počítá s odpadem 10%. - Čtyřboký hranol
Výška pravidelného čtyřbokého hranolu je v = 10 cm, odchylka tělesových úhlopříčky od podstavy je 60°. Určete délku podstavových hran, povrch a objem kvádru. - Plocha stanu
Vypočítejte, kolik plátna (bez podlahy) se spotřebuje na zhotovení stanu, který má tvar pravidelného čtyřbokého jehlanu. Hrana podstavy má délku 3 m a výška stanu je 2m.
Máš příklad, nad kterým si přemýšlíš alespoň 10 minut? Pošli nám příklad a my Ti ho zkusíme vypočítat.
Pythagorova věta je základ výpočtů kalkulačky pravouhlého trojuholníka. Pythagorova věta - příklady. Příklady na čtyřúhelník.
