Příklady na trojúhelník - strana 23 z 124
Počet nalezených příkladů: 2480
- Úhel stoupání
 Velikost úhlu stoupání přímé cesty je přibližně 12 °. Určete stoupání této cesty v procentech.
Velikost úhlu stoupání přímé cesty je přibližně 12 °. Určete stoupání této cesty v procentech. - Přesýpací hodiny
 Přesýpací hodiny sestávají ze dvou shodných nádobek ve tvaru rotačních kuželů. Pro jednoduchost předpokládáme, že koužely se dotýkají pouze svými vrcholy. Písek sahá do poloviny výšky spodního kužele. Po překlopení hodí trvá přesně 21 minut, než se písek
Přesýpací hodiny sestávají ze dvou shodných nádobek ve tvaru rotačních kuželů. Pro jednoduchost předpokládáme, že koužely se dotýkají pouze svými vrcholy. Písek sahá do poloviny výšky spodního kužele. Po překlopení hodí trvá přesně 21 minut, než se písek - Těžiště tetraeder
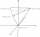 Určete polohu těžiště soustavy čtyř hmotných bodů, které mají hmotnosti, m1, m2 = 2m1, m3 = 3M1 a m4 = 4m1, pokud leží ve vrcholech rovnoramenné tetraedru. (Ve všech případech mezi sousedními hmotnými body je vz
Určete polohu těžiště soustavy čtyř hmotných bodů, které mají hmotnosti, m1, m2 = 2m1, m3 = 3M1 a m4 = 4m1, pokud leží ve vrcholech rovnoramenné tetraedru. (Ve všech případech mezi sousedními hmotnými body je vz - Tři kamarádi 8
 Tři kamarádi sedí na molu, které je přesně uprostřed tekoucí řeky. prvni kamarád se vydává proti proudu řeky rychlostí 0,4 m/s, druhý kamarád se vydává po proudu řeky rychlostí 0,2 m/s, třetí kamarád pluje kolmo směrem ke břehu rychlostí 0,8 m/s. Rychlost
Tři kamarádi sedí na molu, které je přesně uprostřed tekoucí řeky. prvni kamarád se vydává proti proudu řeky rychlostí 0,4 m/s, druhý kamarád se vydává po proudu řeky rychlostí 0,2 m/s, třetí kamarád pluje kolmo směrem ke břehu rychlostí 0,8 m/s. Rychlost - Bombardér
 Z jaké vzdálenosti před cílem musí být z letadla letícího ve výšce 1260 m shozen náklad na padáku, jestliže se snáší rychlostí 5,6 m/s a současně je unášen ve směru pohybu rychlostí 12 m/s. Jaká je přímá vzdálenost letadla od cíle? (Nejdříve si vypočítejt
Z jaké vzdálenosti před cílem musí být z letadla letícího ve výšce 1260 m shozen náklad na padáku, jestliže se snáší rychlostí 5,6 m/s a současně je unášen ve směru pohybu rychlostí 12 m/s. Jaká je přímá vzdálenost letadla od cíle? (Nejdříve si vypočítejt - Látka na šestistěnný stan
 Jeníček s tátou se chystali na stanovačku. Zjistili, že jejich starý stan je již potrhán. Mamka jim navrhla, že jim ušije stan, jehož stěny bude tvořit šest stejných rovnoramenných trojúhelníků. Jejich dolní strana má délku 2 m a výška na tuto stranu měří
Jeníček s tátou se chystali na stanovačku. Zjistili, že jejich starý stan je již potrhán. Mamka jim navrhla, že jim ušije stan, jehož stěny bude tvořit šest stejných rovnoramenných trojúhelníků. Jejich dolní strana má délku 2 m a výška na tuto stranu měří - Součet obsahů
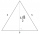 Nád výškou rovnostranného trojúhelníku ABC je sestrojen rovnostranný trojúhelník A1, B1, C1, nad jeho výškou je sestrojen rovnostranný trojúhelník A2, B2, C2, atd. Se postup neustále opakuje. Jaký je velký součet obsahů všech trojúhelníků, pokud strana tr
Nád výškou rovnostranného trojúhelníku ABC je sestrojen rovnostranný trojúhelník A1, B1, C1, nad jeho výškou je sestrojen rovnostranný trojúhelník A2, B2, C2, atd. Se postup neustále opakuje. Jaký je velký součet obsahů všech trojúhelníků, pokud strana tr - Trojboký jehlan
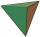 Určete objem a povrch pravidelného trojbokého jehlanu, který má podstavnou hranu a = 20 cm a boční hranu b = 35 cm
Určete objem a povrch pravidelného trojbokého jehlanu, který má podstavnou hranu a = 20 cm a boční hranu b = 35 cm - Zlomený smrk
 Patnactimetrovému smrku ulomila mohutná vichřice vršek tak,že zůstal viset podél zbytku jeho kmene. Vzdálenost tohoto visicího vršku od země byla 4,6 m. V jaké výšce byl kmen smrku zlomen?
Patnactimetrovému smrku ulomila mohutná vichřice vršek tak,že zůstal viset podél zbytku jeho kmene. Vzdálenost tohoto visicího vršku od země byla 4,6 m. V jaké výšce byl kmen smrku zlomen? - Zkratka
 Představte si, že jdete ke kamarádovi po rovné cestě. Ta cesta má délku 350 metrů. Potom zahnete doprava a půjdete dalších 1790 metrů a jste u kamaráda. Otázka zní, o kolik bude kratší cesta, když půjdete přímou cestou přes pole?
Představte si, že jdete ke kamarádovi po rovné cestě. Ta cesta má délku 350 metrů. Potom zahnete doprava a půjdete dalších 1790 metrů a jste u kamaráda. Otázka zní, o kolik bude kratší cesta, když půjdete přímou cestou přes pole? - Ethernet cez ulici
 Karel a Jirka jsou vášniví hráči počítačových her a bydlí v domech, které jsou přesně naproti sobě přes ulici, takže si vidí navzájem do oken. Rozhodli se, že si své počítače propojí telefonním kabelem aby mohli hrát společně hry. Karel bydlí v prvním pat
Karel a Jirka jsou vášniví hráči počítačových her a bydlí v domech, které jsou přesně naproti sobě přes ulici, takže si vidí navzájem do oken. Rozhodli se, že si své počítače propojí telefonním kabelem aby mohli hrát společně hry. Karel bydlí v prvním pat - MIT 1869
 Znáte délku částí 9 a 16, na které přeponu pravoúhlého trojúhelníku rozdělí kolmice spuštěná z jeho protilehlého vrcholu. Úkolem je zjistit délky stran trojúhelníku a délku úsečky x. Tato úloha byla součástí přijímacích zkoušek na Massachusettský technolo
Znáte délku částí 9 a 16, na které přeponu pravoúhlého trojúhelníku rozdělí kolmice spuštěná z jeho protilehlého vrcholu. Úkolem je zjistit délky stran trojúhelníku a délku úsečky x. Tato úloha byla součástí přijímacích zkoušek na Massachusettský technolo - Odvěsna a výška
 Řešte pravoúhlý trojúhelník, je-li dána jeho výška v = 8,5 m a kratší odvěsna b = 15,7 m.
Řešte pravoúhlý trojúhelník, je-li dána jeho výška v = 8,5 m a kratší odvěsna b = 15,7 m. - Úloha o pohybu
 Z křižovatky dvou kolmých silnic vyjeli současně dva cyklisté (každý jinou silnicí) jeden jede průměrnou rychlostí 16 km/h, druhý průměrnou rychlostí 24 km/h. Určete jejich vzájemnou vzdálenost po 25 minutách jízdy.
Z křižovatky dvou kolmých silnic vyjeli současně dva cyklisté (každý jinou silnicí) jeden jede průměrnou rychlostí 16 km/h, druhý průměrnou rychlostí 24 km/h. Určete jejich vzájemnou vzdálenost po 25 minutách jízdy. - Rovnostranný kužel
 Číše má tvar rovnostranného kužele (strana „s” je stejně velká jako průměr jeho podstavy - osový řez je rovnostranný trojúhelník) Má se do něj vejít 0,2 litru kapaliny při výšce hladiny 1cm pod okraj. Vypočítejte jeho průměr
Číše má tvar rovnostranného kužele (strana „s” je stejně velká jako průměr jeho podstavy - osový řez je rovnostranný trojúhelník) Má se do něj vejít 0,2 litru kapaliny při výšce hladiny 1cm pod okraj. Vypočítejte jeho průměr - Nádoba - kužel
 Uzavřená nádoba ve tvaru kužele stojící na své podstavě je naplněna vodou tak, že hladina se nachází 8 cm od vrcholu. Po otočení nádoby o 180 stupňů – stojí na vrcholu – je hladina vzdálena 2 cm od podstavy. Jak vysoká nádoba je?
Uzavřená nádoba ve tvaru kužele stojící na své podstavě je naplněna vodou tak, že hladina se nachází 8 cm od vrcholu. Po otočení nádoby o 180 stupňů – stojí na vrcholu – je hladina vzdálena 2 cm od podstavy. Jak vysoká nádoba je? - MO Z9 2019 domace kolo
 V trojúhelníku ABC leží bod P ve třetině úsečky AB blíže bodu A, bod R je ve třetině úsečky P B blíže bodu P a bod Q leží na úsečce BC tak, že úhly P CB a RQB jsou shodné. Určete poměr obsahů trojúhelníků ABC a PQC.
V trojúhelníku ABC leží bod P ve třetině úsečky AB blíže bodu A, bod R je ve třetině úsečky P B blíže bodu P a bod Q leží na úsečce BC tak, že úhly P CB a RQB jsou shodné. Určete poměr obsahů trojúhelníků ABC a PQC. - Cena plechu na jehlan
 Obvod štvobokého ihlava je 48 m a jeho výška je 2,5 m; kolik bude stát plech na tento jehlan, když 1 m² stojí 1,5 €; do plochy se počítá i 12% ztráta na spoje a záhyby.
Obvod štvobokého ihlava je 48 m a jeho výška je 2,5 m; kolik bude stát plech na tento jehlan, když 1 m² stojí 1,5 €; do plochy se počítá i 12% ztráta na spoje a záhyby. - Kleomurapi
 Kleomurapi je faraón. Jeho stavitelé pyramid si u něj včera stěžovali, že je bolí záda od zvedání kamenů. Faraón tedy nechal postavit rampu dlouhou 6 metrů, širokou 2 metry a vysokou 1,5 metru, aby se stavitelé dostali k druhému patru pyramidy snadněji. K
Kleomurapi je faraón. Jeho stavitelé pyramid si u něj včera stěžovali, že je bolí záda od zvedání kamenů. Faraón tedy nechal postavit rampu dlouhou 6 metrů, širokou 2 metry a vysokou 1,5 metru, aby se stavitelé dostali k druhému patru pyramidy snadněji. K - Počet sázení pro záhon
 Květinový záhon má tvar pravidelného 4-bokého jehlanu. Hrana dolní podstavy je 10m, horní podstavy je 9m. Odchylka boční stěny od podstavy je 45 stupňů. Kolik sázení je třeba nakoupit, pokud k vysazení 1m čtverečního je třeba 90?
Květinový záhon má tvar pravidelného 4-bokého jehlanu. Hrana dolní podstavy je 10m, horní podstavy je 9m. Odchylka boční stěny od podstavy je 45 stupňů. Kolik sázení je třeba nakoupit, pokud k vysazení 1m čtverečního je třeba 90?
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
