Úměra, poměr + podobnost trojúhelníků - příklady a úlohy
Počet nalezených příkladů: 65
- Lichoběžník 83
Lichoběžník ABCD je složen z pěti trojúhelníků. Body E, G dělí úsečku AB v poměru 2:4:3 (v tomto pořadí) na tři úsečky. Bod F je středem úsečky AD. Trojúhelník AEF je rovnoramenný a pravoúhlý. Trojúhelníky GBC a CDG jsou pravoúhlé. Obsah trojúhelníku AEF - Rozhledna 3
Jak vysoká je rozhledna, jestliže vrhá stín dlouhý 9,6m přesně ve stejném okamžiku, kdy puůlmetrová tyč vrhá stín dlouhý 30 cm. - V trojúhelníku 10
V trojúhelníku ABC se velikost vnějšího úhlu při vrcholu C rovná 126°. Velikost vnitřních úhlů při vrcholech A, B jsou v poměru 5: 9. Vypočítej velikost vnitřních úhlů α, β, γ trojúhelníku ABC. - Přesýpací hodiny
Přesýpací hodiny sestávají ze dvou shodných nádobek ve tvaru rotačních kuželů. Pro jednoduchost předpokládáme, že koužely se dotýkají pouze svými vrcholy. Písek sahá do poloviny výšky spodního kužele. Po překlopení hodí trvá přesně 21 minut, než se písek
- Výběr 4
Výběr trojúhelník, který je podobný zadanému trojúhelníku. ∆ RTG, r= 24 dm, t = 28 dm, g= 30 dm. - ∆ SHV= 6 dm, h= 7,5 dm, v= 7 dm - ∆ VSH= v= 7 dm, s= 6 dm, h= 7,5 dm -∆ HVS= h= 7,5 dm, v= 7 dm, s = 6 dm. - ∆ VHS= v= 7 dm, h = 7,5 dm, s= 6 dm. - ∆ HSV= h - Vyber 3
Vyber trojúhelník, který je podobný zadanému trojúhelníku. - ∆ TFC= t= 8 cm, f= 9 cm, c= 7 cm. : ∆ PKU= p= 45 cm, k= 35 cm, u= 40 cm. ∆ UPK= u= 40 cm, p= 45 cm, k= 35 cm. ∆ PUK= p= 45 cm, u= 40 cm, k= 35 cm. ∆ KPU= k= 35 cm, p= 45 cm, u= 40 cm. ∆ KUP= k= - Rozhodni 3 Rozhodni, jestli jsou trojúhelníky podobné. Vyber mezi Ano/Ne. ∆ YUO: y= 9m, u= 17 m, o= 12 m, ∆ ZXV= z= 207 dm, x= 341 dm, v= 394 dm
- Trojúhelníku 80859
Trojúhelník ABC a trojúhelník ADE jsou podobné. Vypočítejte v centimetrech čtverečních obsah trojúhelníku ABC, pokud délka strany DE je 12 cm, délka strany BC je 16 cm a obsah trojúhelníku ADE je 27 cm². - Trojúhelníku 80745 Obsah pravoúhlého trojúhelníku KLM s pravým úhlem u vrcholu L je 60 mm čtverečních a jeho odvěsna k má délku 10 mm. Trojúhelníky KLM a RST jsou podobné, poměr podobnosti je k=2,5 . Vypočítej obsah trojúhelníku RST.
- Náhrdelník 77664
Nicolette vyrábí malý korálkový náramek z 5 červených korálků, 8 fialových korálků a 6 zelených korálků. Velký náhrdelník má stejný poměr korálků jako malý náramek. Pokud velký náhrdelník vyžaduje 15 červených kuliček, kolik fialových kuliček je zapotřebí - Vysokého 73354
Jak dlouhý je stín stromu vysokého 7,6m ak stín 190cm vysoké dopravní značky je dlouhý 3,3m? - Určitou 71544 V parku mladá žena, která je vysoká 1,72 metru, vrhá v určitou hodinu stín vysoký 3,5 metru. Jaká je výška stromu v parku, který zároveň vrhá stín 12,3 metru?
- Trojúhelníku 69144
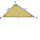Přímka p prochází těžištěm T trojúhelníku a je rovnoběžná s úsečkou BC. Jaký je podíl obsahu rozdělené menší části trojúhelníku přímkou p a obsahu trojúhelníku? - Lichoběžníku 68714
Délka mediánu (střední příčky) lichoběžníku je 10 palců. Medián rozděluje lichoběžník na dvě oblasti, jejichž poměr je 3:5. Délka kratší základny je:
- Délka 15
Délka stínu lípy je 429cm. Délka stínu metrové týče je 78cm. Vypočítej výšku lípy. - Seříznutý kužel
Horní a dolní poloměr seříznutého pravého kruhového kužele je 8 cm a 32 cm. Je-li výška seříznutého okraje 10 cm, jak daleko od spodní základny musí být vytvořena rovina řezu, aby se vytvořily dva podobné seříznuté kužele? - Pětiúhelník
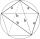Vývěsní štít má tvar pětiúhelníku ABCDE, ve kterém úsečka BC je kolmá na úsečku AB a EA je kolmá na úsečku AB. Bod P je pata kolmice spuštění z bodu D na úsečku AB. |AP|=|PB|, |BC|=|EA|=6dm, |PD|=8,4dm. Na štítu je vyznačen bod X - průsečík úseček PE a DA - Vypočtěte 19
Vypočtěte výšku stromu, který vrhá stín délky 22 m, víte-li, že ve stejném okamžiku pilíř vysoký 2 m vrhá stín dlouhý 3metry. - Velký kužel
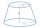Seříznutý rotační kužel má podstavy s poloměry r1 = 8 cm, r2 = 4 cm a výšku v = 5 cm. Jaký je objem kužele, ze kterého komolý kužel vznikl?
Na rovné planině jsou kolmo vzhůru vztyčeny 2 sloupy. Jeden je vysoký 7 m a druhý 4 m. Mezi vrcholem jednoho sloupu a patou druhého sloupu jsou natažena lanka. V jaké výšce se budou lanka křížit? Předpokládejme, že se lanka neprověšují.Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
