Častica 2
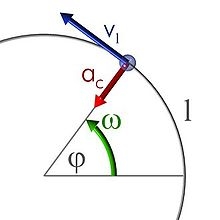
Častica sa začala pohybovať z pokoja po kružnici konštantným uhlovým zrýchlením. Po piatich obehoch (n=5) jej uhlová rýchlosť dosiahla hodnotu ω = 12 rad/s.
Vypočítajte veľkosť uhlového zrýchlenia ε tohto pohybu a časový interval potrebný na prvých 5 obehov.
Vaša odpoveď:
Vypočítajte veľkosť uhlového zrýchlenia ε tohto pohybu a časový interval potrebný na prvých 5 obehov.
Vaša odpoveď:
Tipy na súvisiace online kalkulačky
Chcete premeniť jednotku rýchlosti?
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
algebraplanimetriaJednotky fyzikálnych veličíntémaÚroveň náročnosti úlohy
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Pohyb po kružnici
Hmotný bod sa pohybuje rovnomerne po kružnici s polomerom r=2,7 m uhlovou rýchlosťou ω= 3,3 rad/s. Vypočítajte periódu, frekvenciu a dostredivé zrýchlenie tohto pohybu. - Rotačný pohyb valca
Vypočítajte kinetickú energiu telesa valcovitého tvaru polomeru r= 0,08 metra a hmotnosti m= 1,5 kg v čase t= 5 s, ak sa toto teleso otáča okolo osi idúcej stredom valca s konštantným zrýchlením Ԑ= 5 rad/s², ak v čase t= 0 bolo teleso v pokoji. - Pohyb Lucky
Lucka vyrazila popoludní do skateparku. Pri schádzaní dole z jednoduchej prekážky mala na začiatku v čase t0 = 0 s rýchlosť v0 = 0,6 m/sa každú sekundu pohybu sa jej veľkosť zväčšila o 0,2 m/s. Po 3 s zrýchleného pohybu Lucka pokračovala po rovine rovnome - Zrýchlenie guličky
Guľôčka, ktorú položíme na naklonenú rovinu, sa začne pohybovať a za dobu 5 s dosiahne rýchlosť 1 m/s. Za predpokladu, že pohyb guličky je rovnomerne zrýchlený, určite veľkosť jej zrýchlenia a dráhu, ktorú za uvedený čas prejde. - Družica
Družica obiehajúca okolo Zeme vo výške 800 km má rýchlosť 7,46 km/s. Za akú dobu a s akým veľkým zrýchlením by sa musela pohybovať od štartu až na obežnú dráhu, aby dosiahla túto rýchlosť, keby jej pohyb bol priamočiary rovnomerne zrýchlený? - Polomerom a pretekár
Pretekár beží po kruhovej dráhe s polomerom 86 m, koľko metrov ubehne pri piatich obehoch. (Riešenie a podrobný postup) - Automobil 8
Automobil dosiahne rovnomerným zrýchlením za 24 s z pokoja rýchlosť 100 km/h. Akú dráhu pri rozjazde dosiahne?
