Voľný pád Penny
Muž zhodil cent z vrcholu 500 metrov vysokej budovy. Po t sekundách cent klesol o vzdialenosť s metrov, kde s(t)=500-5t2 . Určte priemernú rýchlosť medzi 1 s a 5 s.
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
základné operácie a pojmyJednotky fyzikálnych veličíntémaÚroveň náročnosti úlohy
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Pozorovací uhol
 Z bodu A na zemi je pozorovací uhol vrcholu 20 m vysokej budovy 45°. Na vrchole budovy je vztýčená vlajka a pozorovací uhol vrcholu vlajkovej tyče od A je 60°. Nájdite dĺžku vlajkovej tyče a vzdialenosť budovy od bodu A.
Z bodu A na zemi je pozorovací uhol vrcholu 20 m vysokej budovy 45°. Na vrchole budovy je vztýčená vlajka a pozorovací uhol vrcholu vlajkovej tyče od A je 60°. Nájdite dĺžku vlajkovej tyče a vzdialenosť budovy od bodu A. - Z vrcholu
 Z vrcholu veže vysokej 80m je vrhnuté vodorovným smerom teleso začiatočnou rýchlosťou veľkosti 15 m/s. Za aký čas a v akej vzdialenosti od päty veže dopadne teleso na vodorovný povrch Zeme? (použite g = 10 m/s²)
Z vrcholu veže vysokej 80m je vrhnuté vodorovným smerom teleso začiatočnou rýchlosťou veľkosti 15 m/s. Za aký čas a v akej vzdialenosti od päty veže dopadne teleso na vodorovný povrch Zeme? (použite g = 10 m/s²) - Stredy tetív
 Kružnica s priemerom 17cm, hornou tetivou |CD| = 10,2cm a dolnou tetivou |EF| = 7,5cm, kde pre stredy tetív H, G platí |EH| = 1/2 |EF| a |CG| = 1/2 |CD|, určte vzdialenosť medzi bodom G a H. CD II EF.
Kružnica s priemerom 17cm, hornou tetivou |CD| = 10,2cm a dolnou tetivou |EF| = 7,5cm, kde pre stredy tetív H, G platí |EH| = 1/2 |EF| a |CG| = 1/2 |CD|, určte vzdialenosť medzi bodom G a H. CD II EF. - Rádiova anténa
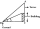 Avanti sa snaží nájsť výšku rádiovej antény na streche miestnej budovy. Stojí vo vodorovnej vzdialenosti 21 metrov od budovy. Uhol elevácie od jej očí k streche (bod A) je 42° a uhol elevácie od jej očí k vrcholu antény (bod B) je 51°. Ak sú jej oči 1,54
Avanti sa snaží nájsť výšku rádiovej antény na streche miestnej budovy. Stojí vo vodorovnej vzdialenosti 21 metrov od budovy. Uhol elevácie od jej očí k streche (bod A) je 42° a uhol elevácie od jej očí k vrcholu antény (bod B) je 51°. Ak sú jej oči 1,54 - Strelec
 Strelec počul náraz strely na terč za 1s po výstrele. Strela sa pohybovala priemernou rýchlosťou 500 m/s. Počítajte s rýchlosťou zvuku 340 m/s. Určte vzdialenosť terča.
Strelec počul náraz strely na terč za 1s po výstrele. Strela sa pohybovala priemernou rýchlosťou 500 m/s. Počítajte s rýchlosťou zvuku 340 m/s. Určte vzdialenosť terča. - Častica
 Častica sa pohybuje v priamke tak, že jej rýchlosť (m/s) v čase t sekúnd je daná vzťahom v (t) = 3t2-4t-4, t > 0. Spočiatku je častica 8 metrov vpravo od pevného pôvodu. Po koľkých sekundách je častica na začiatku?
Častica sa pohybuje v priamke tak, že jej rýchlosť (m/s) v čase t sekúnd je daná vzťahom v (t) = 3t2-4t-4, t > 0. Spočiatku je častica 8 metrov vpravo od pevného pôvodu. Po koľkých sekundách je častica na začiatku? - Auto 7
 Auto prešlo vzdialenosť medzi mestami A a B za 4 hodiny, keby priemernú rýchlosť sme zvýšili o 17km/h prešlo by auto túto vzdialenosť o hodinu skôr. Určte pôvodnú rýchlosť auta a vzdialenosť medzi mestami A, B.
Auto prešlo vzdialenosť medzi mestami A a B za 4 hodiny, keby priemernú rýchlosť sme zvýšili o 17km/h prešlo by auto túto vzdialenosť o hodinu skôr. Určte pôvodnú rýchlosť auta a vzdialenosť medzi mestami A, B.
