Delenie buniek
Na záver by sme si mohli dať niečo jednoduchšie a tak trochu (aspoň matematicky) zábavnejšie…
Na začiatku nebolo nič... Ale nie, tu máme na začiatku jednu jedinú bunku. Táto bunka nie je len taká obyčajná bunka, je zvláštna, pretože je o nej matematická úloha – a preto sa delí špeciálne – vždy na osem rovnakých buniek a tie sa potom znovu môžu rozdeliť na osem rovnakých buniek (z jednej máme po delení osem) – ale pozor, vždy sa všetky bunky rozdelia naraz. ..
Je možné, aby v jednom okamihu existovalo presne 2010 buniek?
A nie, naozaj nebudeme uvažovať akýsi kratinký okamih počas delenia buniek. Ak sa bunky rozdelia vždy po troch hodinách, po koľkých hodinách od prvého delenia by taký stav – 2010 existujúcich buniek (ale iba pokiaľ je možný) nastal?
Vaša odpoveď:
Na začiatku nebolo nič... Ale nie, tu máme na začiatku jednu jedinú bunku. Táto bunka nie je len taká obyčajná bunka, je zvláštna, pretože je o nej matematická úloha – a preto sa delí špeciálne – vždy na osem rovnakých buniek a tie sa potom znovu môžu rozdeliť na osem rovnakých buniek (z jednej máme po delení osem) – ale pozor, vždy sa všetky bunky rozdelia naraz. ..
Je možné, aby v jednom okamihu existovalo presne 2010 buniek?
A nie, naozaj nebudeme uvažovať akýsi kratinký okamih počas delenia buniek. Ak sa bunky rozdelia vždy po troch hodinách, po koľkých hodinách od prvého delenia by taký stav – 2010 existujúcich buniek (ale iba pokiaľ je možný) nastal?
Vaša odpoveď:
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
algebraaritmetikazákladné operácie a pojmyÚroveň náročnosti úlohy
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Myška Hryzka
Myška Hryzka našla 27 rovnakých kociek syra. Najskôr si z nich poskladala veľkú kocku a chvíľu počkala, než sa syrové kocôčky k sebe prilepili. Potom z každej steny veľkej kocky vyhryzie strednú kocôčku. Potom zjedla aj kocôčky, ktorá bola v stredu veľkej - Miško 3
Miško dostal taký počet cukríkov, že všetky cifry v tomto počte boli rovnaké. Dokážte, že vždy pokiaľ vie takýto počet cukríkov rozdeliť na 72 rovnakých kôpok, tak ich vie rozdeliť aj na 37 rovnakých kôpok. (Pozn. : cukríky nevieme rozlomiť) - Brigádnici 11
Brigádnici nazbierali 268 kg jabĺk a musia ich roztriediť do košov po 7 kg. Podari sa im jablka presne rozdeliť? Budú všetky koše doplná naplnené? Koľko košov budú potrebovať, ak chcú všetky jablká dať do košov - Petriho miska
Petriho miska obsahuje 35 buniek. Každý deň sa každá bunka v Petriho miske rozdelí na 2 bunky procesom mitózy. Koľko buniek je tam po 14 dňoch? - Roboti Z7
V škole pre robotov do jednej triedy chodí dvadsať robotov Robertov, ktorí sú očíslovaní Robert 1 až Robert 20. V triede je práve napätá atmosféra, rozprávajú sa spolu iba niektorí roboti. Roboti s nepárnym číslom sa nerozprávajú s robotmi s párnym číslom - Zapojenie žiaroviek
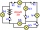Tu máš úlohu tak trochu na premýšľanie, ale veľkú zložitosť v tom nehľadaj. Máš tu zapojených 6 žiaroviek A až F a 6 spínačov č. 1 až č. 6. Tvojou úlohou bude postupne určiť, ktoré žiarovky budú vždy svietiť, pokiaľ bude niektorý zo spínačov v polohe vypn - Hájny
Hajný sledoval z lesného posedu srny. V jednom okamihu ich mohli zazrieť 6. Koľko najviac srniek mohli v tom istom okamihu zahliadnuť traja hájný.
