MAKS 6
V Budáni je osem miest, z ktorých niektore su pospajane cestami. Na kazdom mieste kde cesta vychadza alebo vchadza do mesta je brana. Ziadne dve cesty sa nekrizuju ani nevchadzaju tou istou branou. Pocet bran sa zhoduje jednou z cisiel 5,15,21,24 alebo 27. Kolko je v Budani ciest a mestskych bran.
Správna odpoveď:

Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Z mesta 3
 Z mesta A do mesta B vedú 4 cesty. Z mesta B do mesta C vedie 5 ciest. Koľkými rôznymi cestami vieme prísť z mesta A do mesta C cez mesto B?
Z mesta A do mesta B vedú 4 cesty. Z mesta B do mesta C vedie 5 ciest. Koľkými rôznymi cestami vieme prísť z mesta A do mesta C cez mesto B? - Turistických 70204
 Z parkoviska je možné na vrchol kopca vystúpiť po troch rôznych turistických trasách alebo vyjsť lanovkou a rovnakými štyrmi spôsobmi je možné zostúpiť z kopca späť na parkovisko, ako ilustruje obrázok. Cestou na vrchol kopca a späť je myslený výstup a zo
Z parkoviska je možné na vrchol kopca vystúpiť po troch rôznych turistických trasách alebo vyjsť lanovkou a rovnakými štyrmi spôsobmi je možné zostúpiť z kopca späť na parkovisko, ako ilustruje obrázok. Cestou na vrchol kopca a späť je myslený výstup a zo - Z mesta 4
 Z mesta A do mesta B vedie 5 ciest, z mesta B do mesta C vedú 3 cesty a z mesta C do mesta D vedú 4 cesty. Určte počet ciest, ktoré vedú z A do D cez B a C.
Z mesta A do mesta B vedie 5 ciest, z mesta B do mesta C vedú 3 cesty a z mesta C do mesta D vedú 4 cesty. Určte počet ciest, ktoré vedú z A do D cez B a C. - Z obce
 Z obce A do obce B vedie peť ciest, z obce B do obce C vedú dve cesty a z obce A do obce C vedie priamo len jedna cesta. Koľkými rôznymi spôsobmi sa dá dostať: A) z obce A do obce C cez obec B? B) akokoľvek z obce A do obce C? C) akokoľvek z obce A do obc
Z obce A do obce B vedie peť ciest, z obce B do obce C vedú dve cesty a z obce A do obce C vedie priamo len jedna cesta. Koľkými rôznymi spôsobmi sa dá dostať: A) z obce A do obce C cez obec B? B) akokoľvek z obce A do obce C? C) akokoľvek z obce A do obc
- Zo Zubrohlavy
 Zo Zubrohlavy do Bobrova vedie jedna asfaltová cesta, dve lesné cesty a jedna cyklocesta. Určite počet spôsobov, ktorými sa dostaneme zo Zubrohlavy do Bobrova a späť. Vypíšte všetky možnosti.
Zo Zubrohlavy do Bobrova vedie jedna asfaltová cesta, dve lesné cesty a jedna cyklocesta. Určite počet spôsobov, ktorými sa dostaneme zo Zubrohlavy do Bobrova a späť. Vypíšte všetky možnosti. - Tri mestá a sedem ciest
 Ak sú 3 cesty z mesta A do mesta B a 4 cesty z mesta B do mesta C, koľkými spôsobmi sa dá ísť z mesta A do mesta C a späť do mesta A cez mesto B bez toho, aby ste prechádzali rovnakou cestou dvakrát?
Ak sú 3 cesty z mesta A do mesta B a 4 cesty z mesta B do mesta C, koľkými spôsobmi sa dá ísť z mesta A do mesta C a späť do mesta A cez mesto B bez toho, aby ste prechádzali rovnakou cestou dvakrát? - Medzi 11
 Medzi dvoma mestami na pobreží Chorvátska je vodorovná vzdialenosť 9 km. Cesta spájajúca tieto dve mestá má stúpanie 13 promile. Aký je výškový rozdiel chorvátskych miest?
Medzi dvoma mestami na pobreží Chorvátska je vodorovná vzdialenosť 9 km. Cesta spájajúca tieto dve mestá má stúpanie 13 promile. Aký je výškový rozdiel chorvátskych miest? - Dve horárne
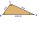 Dve horárne A, B sú oddelené lesom, obe sú viditeľné z horárne C, ktorá je s oboma spojená priamymi cestami. Akú bude mať dĺžku projektovaná cesta z A do B, ak je AC = 5004 m, BC = 2600 m a uhol ABC = 53° 45 '?
Dve horárne A, B sú oddelené lesom, obe sú viditeľné z horárne C, ktorá je s oboma spojená priamymi cestami. Akú bude mať dĺžku projektovaná cesta z A do B, ak je AC = 5004 m, BC = 2600 m a uhol ABC = 53° 45 '? - Na ihrisku 2
 Na ihrisku sú nakreslené tri rovnako veľké kruhy. Rozostavte 16 kolkov tak, aby v každom kruhu stálo 9 kolkov. Nájdite aspoň osem podstatne odlišných rozostavení, t. J. takých rozostavení, pri ktorých sa nerozlišujú kolky ani kruhy.
Na ihrisku sú nakreslené tri rovnako veľké kruhy. Rozostavte 16 kolkov tak, aby v každom kruhu stálo 9 kolkov. Nájdite aspoň osem podstatne odlišných rozostavení, t. J. takých rozostavení, pri ktorých sa nerozlišujú kolky ani kruhy.
- Vzdialených 20483
 Kedy a kde sa stretnú dve autá, ktoré vyjazdili súčasne proti sebe z miest A a B vzdialených 90 km, ak auto zo mesta A jede rýchlosťou 75 km/ha auto z mesta B rýchlosťou 60 km/h?
Kedy a kde sa stretnú dve autá, ktoré vyjazdili súčasne proti sebe z miest A a B vzdialených 90 km, ak auto zo mesta A jede rýchlosťou 75 km/ha auto z mesta B rýchlosťou 60 km/h? - Denis
 Denis odišiel z mesta L do mesta M konštantnou rýchlosťou a cesta mu trvala 10 hodín. V rovnakom čase Samuel odišiel z mesta M do mesta L a cestoval konštantnou rýchlosťou a cesta trvala 6 hodín. Obaja sa minuli v bode 72 km od mesta L. a) Aká je vzdialen
Denis odišiel z mesta L do mesta M konštantnou rýchlosťou a cesta mu trvala 10 hodín. V rovnakom čase Samuel odišiel z mesta M do mesta L a cestoval konštantnou rýchlosťou a cesta trvala 6 hodín. Obaja sa minuli v bode 72 km od mesta L. a) Aká je vzdialen - Dvaja cyklisti
 Súčasne dvaja cyklisti opustili mestá A a B pri konštantných rýchlostiach. Prvý z mesta A do mesta B a druhý z mesta B do mesta A. Na jednom mieste cesty sa stretli. Po stretnutí prvý cyklista prišiel do mesta B za 36 minút, druhý cyklista prišiel do mest
Súčasne dvaja cyklisti opustili mestá A a B pri konštantných rýchlostiach. Prvý z mesta A do mesta B a druhý z mesta B do mesta A. Na jednom mieste cesty sa stretli. Po stretnutí prvý cyklista prišiel do mesta B za 36 minút, druhý cyklista prišiel do mest - V hoteli 2
 V hoteli Holiday majú na každom poschodí rovnaký počet izieb. Izby sú číslované prirodzenými číslami postupne od prvého poschodia, žiadne číslo nie je vynechané a každá izba má iné číslo. Do hotela pricestovali traja turisti. Prvý sa ubytoval v izbe číslo
V hoteli Holiday majú na každom poschodí rovnaký počet izieb. Izby sú číslované prirodzenými číslami postupne od prvého poschodia, žiadne číslo nie je vynechané a každá izba má iné číslo. Do hotela pricestovali traja turisti. Prvý sa ubytoval v izbe číslo - Počet detí v rodine
 V triede sme zisťovali, koľko detí majú rodine, v ktorých žijeme. Koľko % žiakov žije v rodine s viac ako 2 deťmi, ak v 5 rodinách majú po 1 dieťati, v 9 rodinách majú po dve deti, v 5 rodinách majú po 3 deti, v 2 rodinách majú po 4 deti, v jednej rodine
V triede sme zisťovali, koľko detí majú rodine, v ktorých žijeme. Koľko % žiakov žije v rodine s viac ako 2 deťmi, ak v 5 rodinách majú po 1 dieťati, v 9 rodinách majú po dve deti, v 5 rodinách majú po 3 deti, v 2 rodinách majú po 4 deti, v jednej rodine
- Mestá
 Auto išlo z A. do B 4h. Pri spiatočnej ceste išlo auto rýchlosťou o 15km/h väčšou. Spiatočná cesta preto trvala o 48 min. kratšie ako cesta tam. Urč vzdialenosť miest.
Auto išlo z A. do B 4h. Pri spiatočnej ceste išlo auto rýchlosťou o 15km/h väčšou. Spiatočná cesta preto trvala o 48 min. kratšie ako cesta tam. Urč vzdialenosť miest. - Počet bodov
 V koľkých bodoch sa pretne 10 priamok, ak žiadne dve nie sú rovnobežné?
V koľkých bodoch sa pretne 10 priamok, ak žiadne dve nie sú rovnobežné? - Vzdialenosť 3166
 Cesta vedúca z miesta A do B má stúpanie 9%. Určte vodorovnú vzdialenosť týchto dvoch miest za predpokladu, že rozdiel ich nadmorských výšok je 27,9 m.
Cesta vedúca z miesta A do B má stúpanie 9%. Určte vodorovnú vzdialenosť týchto dvoch miest za predpokladu, že rozdiel ich nadmorských výšok je 27,9 m.
