Goniometria a trigonometria - slovné úlohy a príklady - strana 31 z 32
Počet nájdených príkladov: 626
- Trojuholník 97
Trojuholník DEF s Ê=40°, F=90° EF = 45 mm. Zmerajte DE. - Veža + stožiar
Na vodorovnej rovine je zvislá veža s vlajkovou tyčou na jej vrchole. V bode vzdialenom 9 m od päty veže je uhol elevácie hornej a dolnej časti vlajkovej tyče 60° a 30°. Nájdite výšku stožiaru vlajky. - Trojuholník - výkres
Nájdite dĺžku úsečky x v daných výkresoch trojuholníka. - Pozorovací uhol
Dvaja muži sú na opačných stranách veže. Namerajú uhly elevácie (pozorovací) vrcholu veže ako 30° a druhý ako 45°. Ak je výška veže 50 m, nájdite vzdialenosť medzi týmito dvoma mužmi. - Vzdialenosť veže
Pozorovací uhol vrcholu veže od bodu A na zemi je 30°. Pri presune na vzdialenosť 20 m smerom k päte veže do bodu B sa pozorovací uhol zväčší na 60°. Nájdite výšku veže a vzdialenosť veže od miesta A . - Uhol elevácie 3
Uhol elevácie tyče z bodu na vodorovnej zemi je 15°. Po prekonaní vzdialenosti 10 m smerom k tyči sa uhol elevácie zmení na 30°. Aká je výška tyče? - Pozorovací uhol
Z bodu A na zemi je pozorovací uhol vrcholu 20 m vysokej budovy 45°. Na vrchole budovy je vztýčená vlajka a pozorovací uhol vrcholu vlajkovej tyče od A je 60°. Nájdite dĺžku vlajkovej tyče a vzdialenosť budovy od bodu A. - Kosoštvorec - uhly
Kosoštvorec ABCD so stranou dlhou 8 cm má uhlopriečku BD dlhú 11,3 cm. Nájdite uhol DAB. - Tri domy
Tri domy tvoria trojuholníkový tvar. Dom A je 50 stôp od domu C a dom B je 60 stôp od domu C. Uhol ABC je 45 stupňov. Nakreslite obrázok a nájdite vzdialenosť medzi A a B. - Tieň 2
Tieň veže stojacej na rovnom povrchu je o 40 m dlhší, keď je výška Slnka 30°, ako keď je 60°. Nájdite výšku veže. - Búrka zlomí
Strom sa vplyvom búrky zlomí a zlomená časť sa ohne tak, že sa vrchol stromu dotkne zeme a zviera s ním uhol 30°. Vzdialenosť medzi pätou stromu a bodom, kde sa vrchol dotýka zeme, je 8 m. Nájdite výšku stromu. - Drôt okolo trojuholníku Kus drôtu je ohnutý do tvaru trojuholníka. Dve strany majú dĺžku 24 palcov a 21 palcov. Uhol medzi týmito dvoma stranami je 55°. Aká je dĺžka tretej strany s presnosťou na stotiny palca? Odpoveď: Dĺžka tretej strany je približne ____ palcov.
- Maják - východ
Maják má výhľad na záliv a je vysoký 77 metrov. Z vrchu môže strážca majáku vidieť jachtu na juh pod hĺbkovým uhlom (uhol depresie) 32 stupňov a ďalšiu loď na východ pod uhlom 25 stupňov. Aká je vzdialenosť medzi člnmi? - Pilier
Uhol sklonu vrcholu nedokončeného piliera v bode 150 m od jeho základne je 30°. Ak má byť uhol elevácie v tom istom bode 45°, potom sa musí stĺp zdvihnúť do výšky o koľko metrov? - Šiesta mocnina zet
Nech z = 2 - sqrt(3i). Nájdite z6 a vyjadrite svoju odpoveď v pravouhlom tvare komplexného čísla. Ak z = 2 - 2sqrt(3 i), potom r = |z| = sqrt(2 ^ 2 + (- 2sqrt(3)) ^ 2) = sqrt(16) = 4 a theta = tan -2√3/2=-π/3 - Verzor - polárna forma
Vyriešte nasledujúci výpočet komplexných verzorov - 5,2∠58° - 1,6∠-40° a dajte odpoveď v polárnej forme - Kosínusova - rameno
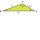Pomocou kosínusovej vety nájdite dĺžku ramena b, ak sú dané hodnoty uhla β=20°, a strán a=10 a c=15. - Pravidelný decadon
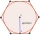Apotém pravidelného šesťuholníka je 5√3 palcov. Nájdite jednu z jeho strán a jeho obsah. - Trojuholníkový pozemok
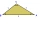Trojuholníkový pozemok má rozmery a=15m, b=10m a c=20m. Aká je veľkosť uhla medzi stranami b a c? - ABCD kosoštvorec
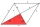ABCD je kosoštvorec so stranami 10,5 cm. Ak je dĺžka uhlopriečky AC = 15,8 cm, použite kosínusový vzorec. a. vypočítajte dĺžku uhlopriečky BD s presnosťou na najbližší cm b. uhly kosoštvorca s presnosťou na najbližší stupeň.
Máš príklad, ktorý si tu nenašiel vyriešenú? Pošli nám príklad a my Ti ho skúsime vypočítať.
