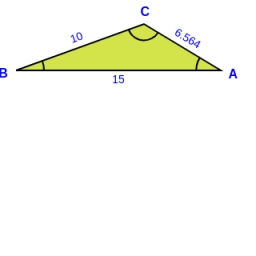
Kosínusova - rameno
Pomocou kosínusovej vety nájdite dĺžku ramena b, ak sú dané hodnoty uhla β=20°, a strán a=10 a c=15.
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Pytagorova veta je základ výpočtov aj kalkulačky pravouhlého trojuholníka.
Kosínusovú vetu priamo používa kalkulačka SUS trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Kosínusovú vetu priamo používa kalkulačka SUS trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
aritmetikaplanimetriagoniometria a trigonometriaJednotky fyzikálnych veličínÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Tri palice
Loonie má tri drevené palice s rozmermi 17 palcov, 21 palcov a 25 palcov. Položí ich tak, aby vytvorili trojuholník. Nájdite veľkosť uhla ohraničeného stranami 17 palcov a 21 palcov. (Vyjadrite odpovede s presnosťou na stotiny) (pomocou kosínusovej vety) - Ťažisko a obsah
V trojuholníku ABC sú dané dĺžky jeho ťažníc tc=9, ta=6. Označme T priesečník ťažníc, S stred strany BC. Veľkosť uhla CTS je 60°. Vypočítajte dĺžku strany BC s presnosťou na 2 desatinné miesta - Uhol alfa
Pravouhlý trojuholník. Je dané: strana c=15,8 a uhol alfa=73°10' Výpočítate stranu a, b, uhol beta a obsah. - Narysujte
Narysujte rovnoramenný trojuholník ABC, ak AB=7cm, veľkosť uhla ABC je 47°, ramená |AC| = |BC|. Odmerajte veľkosť strany BC v mm. - Štvoruholník - uhly
Výpočty z geometrie: Pomery strán štvoruholníka sú 3:6:4,5:3,5. Vypočítajte ich dĺžky, ak obvod je 51 cm. Veľkosti uhlov v štvoruholníku sú = 29°30', = 133°10',= 165°20'. Aká je veľkosť uhla D? - RR lichobeznik 8
Zostroj rovnoramenný lichobežník, ktorého základňa má dĺžku 6cm, zviera s uhlopriečkou uhol 30° a ramená majú dĺžku 4cm. - Funkcie sinus, kosinus
Vypočítaj veľkosti zostávajúcich strán a uhlov pravouhlého trojuholníka ABC, ak je dané: b = 10 cm; c = 20 cm; uhol alfa = 60° a uhol beta = 30° (použi Pytagorova vetu a funkcie sínus, kosínus, tangens, kotangens)
