Príklady na obsah uhol - strana 10 z 14
Počet nájdených príkladov: 263
- Šesťuholník nepravidelný
 Na obrázku je štvorec ABCD, štvorec EFGD a obdĺžnik HIJD. Body J a G ležia na strane CD, pričom platí |DJ| < |DG| a body H a E ležia na strane DA, pričom platí /DH/ < /DE/. Ďalej vieme, že/DJ/ = /GC/. Šesťuholník ABCGFE má obvod 96 cm, šesťuholník E
Na obrázku je štvorec ABCD, štvorec EFGD a obdĺžnik HIJD. Body J a G ležia na strane CD, pričom platí |DJ| < |DG| a body H a E ležia na strane DA, pričom platí /DH/ < /DE/. Ďalej vieme, že/DJ/ = /GC/. Šesťuholník ABCGFE má obvod 96 cm, šesťuholník E - Koza
 Je lúka tvaru kruhu r = 24 m. Ako dlhý musí byť povraz na uviazanie kozy ku kolíku na obvode lúky, aby spásla len polovicu lúky?
Je lúka tvaru kruhu r = 24 m. Ako dlhý musí byť povraz na uviazanie kozy ku kolíku na obvode lúky, aby spásla len polovicu lúky? - Štvorboký ihlan
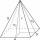 Aký je povrch pravidelného štvorbokého ihlanu, keď je podstavná hrana a=21 a výška v=13?
Aký je povrch pravidelného štvorbokého ihlanu, keď je podstavná hrana a=21 a výška v=13? - Kúžeľ S2V
 Plášť kužeľa rozvinutý do roviny má tvar kruhového výseku so stredovým uhlom 126° a obsahom 415 mm². Vypočítajte objem tohto kužeľa.
Plášť kužeľa rozvinutý do roviny má tvar kruhového výseku so stredovým uhlom 126° a obsahom 415 mm². Vypočítajte objem tohto kužeľa. - Do kužeľa
 Do kužeľa je vpísaná guľa (prienik ich hraníc sa skladá z kružnice a jedného bodu). Pomer povrchu gule a obsahu podstavy je 4:3. Rovina, ktorá prechádza osou kužeľa, reže kužeľ v rovnoramennom trojuholníku. Určte veľkosť uhla oproti základni tohto trojuho
Do kužeľa je vpísaná guľa (prienik ich hraníc sa skladá z kružnice a jedného bodu). Pomer povrchu gule a obsahu podstavy je 4:3. Rovina, ktorá prechádza osou kužeľa, reže kužeľ v rovnoramennom trojuholníku. Určte veľkosť uhla oproti základni tohto trojuho - Šikmá strecha
 Strecha veže má tvar pravidelného štvorbokého ihlana, ktorého podstavná hrana je dlhá 11 m a bočná stena zviera s podstavou uhol veľkosti 57°. Vypočítajte koľko krytiny potrebujeme na pokrytie celej strechy, ak počítame s 15%-ným odpadom.
Strecha veže má tvar pravidelného štvorbokého ihlana, ktorého podstavná hrana je dlhá 11 m a bočná stena zviera s podstavou uhol veľkosti 57°. Vypočítajte koľko krytiny potrebujeme na pokrytie celej strechy, ak počítame s 15%-ným odpadom. - Bazénik
 Dno detského bazéniku je pravidelný šesťuholník so stranou a = 60 cm. Vzdialenosť protilahlých strán je 104cm, výška bazéniku je 45cm. A) Koľko litrov vody sa zmestí do bazéniku? B) Bazénik je vyrobený z dvojitej vrstvy plastovej fólie. Minimálne koľko m²
Dno detského bazéniku je pravidelný šesťuholník so stranou a = 60 cm. Vzdialenosť protilahlých strán je 104cm, výška bazéniku je 45cm. A) Koľko litrov vody sa zmestí do bazéniku? B) Bazénik je vyrobený z dvojitej vrstvy plastovej fólie. Minimálne koľko m² - Tvrdé drevo
 Tvrdé drevo pre stĺp je v tvare zrezaného ihlana, pravidelnej heptagonálnej (hepta=7) pyramídy. Dolná hrana základne je 18 cm a horná základňa 14 cm. Výška je 30 cm. Zistite jeho hmotnosť v kg, ak je hustota dreva 10 gramov/cm³.
Tvrdé drevo pre stĺp je v tvare zrezaného ihlana, pravidelnej heptagonálnej (hepta=7) pyramídy. Dolná hrana základne je 18 cm a horná základňa 14 cm. Výška je 30 cm. Zistite jeho hmotnosť v kg, ak je hustota dreva 10 gramov/cm³. - Kruhový bazén
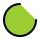 Podstava bazéna má tvar kruhu s polomerom r=10m okrem kruhového odseku, ktorý určuje tetiva dĺžky 10m. Jeho hĺbka je h=2m. Koľko hektolitrov vody sa zmesti do bazéna?
Podstava bazéna má tvar kruhu s polomerom r=10m okrem kruhového odseku, ktorý určuje tetiva dĺžky 10m. Jeho hĺbka je h=2m. Koľko hektolitrov vody sa zmesti do bazéna? - Astronaut
 Aké percento zemského povrchu vidí astronaut z výšky h = 350 km. Zoberme Zem ako guľu s polomerom R = 6370 km
Aké percento zemského povrchu vidí astronaut z výšky h = 350 km. Zoberme Zem ako guľu s polomerom R = 6370 km - Strecha domu
 Strecha domu má tvar pravidelného štvorbokého ihlana s podstavnou hranou 11 m. Koľko m² je potrebné na jej pokrytie ak sklon strechy je 30 ° a na spoje a odpad počítame 9% plechu navyše?
Strecha domu má tvar pravidelného štvorbokého ihlana s podstavnou hranou 11 m. Koľko m² je potrebné na jej pokrytie ak sklon strechy je 30 ° a na spoje a odpad počítame 9% plechu navyše? - Štvorboký ihlan - objem a povrch
 V pravidelnom štvorbokom ihlane je výška 6,5 cm a uhol medzi podstavou a bočnou stenou je 42°. Vypočítaj povrch a objem telesa. Výpočty zaokrúhliť na 1 desatinné miesto.
V pravidelnom štvorbokom ihlane je výška 6,5 cm a uhol medzi podstavou a bočnou stenou je 42°. Vypočítaj povrch a objem telesa. Výpočty zaokrúhliť na 1 desatinné miesto. - Kosý hranol
 Aký objem má štvorboký kosý hranol s podstavnými hranami o dĺžke a = 1m, b = 1,1m, c = 1,2 m, d = 0,7m, ak bočná hrana s dĺžkou h = 3,9 m má odchýlku od podstavy 20°35' a hrany a, b zvierajú uhol 50,5°?
Aký objem má štvorboký kosý hranol s podstavnými hranami o dĺžke a = 1m, b = 1,1m, c = 1,2 m, d = 0,7m, ak bočná hrana s dĺžkou h = 3,9 m má odchýlku od podstavy 20°35' a hrany a, b zvierajú uhol 50,5°? - Zemeguľa
 Koľko percent zemského povrchu leží v pásme tropickom, miernom, arktickom? Hranicu medzi pásmami tvoria rovnobežky 23°27´ a 66°33´.
Koľko percent zemského povrchu leží v pásme tropickom, miernom, arktickom? Hranicu medzi pásmami tvoria rovnobežky 23°27´ a 66°33´. - Zrezaný ihlan 2
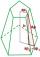 Vypočítajte objem pravidelného šesťbokého zrezaného ihlana, ak je dĺžka hrany dolnej podstavy 30 cm, hornej podstavy 12 cm a ak dĺžka bočnej hrany je 41 cm.
Vypočítajte objem pravidelného šesťbokého zrezaného ihlana, ak je dĺžka hrany dolnej podstavy 30 cm, hornej podstavy 12 cm a ak dĺžka bočnej hrany je 41 cm. - Štvorboký ihlan
 Koľko metrov štvorcových je potreba na pokrytie veže tvaru pravidelného štvorbokého ihlanu o podstavnej hrane 10 metrov, ak je odchýlka bočnej hrany od roviny podstavy 68°? Pri pokrytí sa počíta s odpadom 10%.
Koľko metrov štvorcových je potreba na pokrytie veže tvaru pravidelného štvorbokého ihlanu o podstavnej hrane 10 metrov, ak je odchýlka bočnej hrany od roviny podstavy 68°? Pri pokrytí sa počíta s odpadom 10%. - Podstava RR licho
 Podstavou hranola je rovnoramenný lichobežník ABCD sa základňami AB = 12 cm, CD = 9 cm. Uhol pri vrchole B je 48° 10'. Určte objem a porch hranolov, ak je jeho výška 35 cm.
Podstavou hranola je rovnoramenný lichobežník ABCD sa základňami AB = 12 cm, CD = 9 cm. Uhol pri vrchole B je 48° 10'. Určte objem a porch hranolov, ak je jeho výška 35 cm. - Objem 40
 Objem kvádra so štvorcovou podstavovou je 64 cm³ a odchýlka telesovej uhlopriečky od roviny podstavy je 45 stupňov. Vypočítajte jeho povrch.
Objem kvádra so štvorcovou podstavovou je 64 cm³ a odchýlka telesovej uhlopriečky od roviny podstavy je 45 stupňov. Vypočítajte jeho povrch. - Sklársky príklad
 Koľko skla potrebujeme na vyrobu pohara s podstavou pravidelneho 5 uholnika ak obsah 1 trojuholnika v postave je 4,2 cm² a vyška telesa je 10 cm?
Koľko skla potrebujeme na vyrobu pohara s podstavou pravidelneho 5 uholnika ak obsah 1 trojuholnika v postave je 4,2 cm² a vyška telesa je 10 cm? - Spotreba papiera
 Vypočítaj spotrebu papiera na krabicu tvaru štvorbokého hranola s kosoštvorcovou podstavou, podstavná hrana a = 6cm, susediace hrany zvierajú uhol alfa = 60°. Výška krabice je 10cm. Koľko m² papiera spotrebujeme na 100 takých krabíc?
Vypočítaj spotrebu papiera na krabicu tvaru štvorbokého hranola s kosoštvorcovou podstavou, podstavná hrana a = 6cm, susediace hrany zvierajú uhol alfa = 60°. Výška krabice je 10cm. Koľko m² papiera spotrebujeme na 100 takých krabíc?
Máš úlohu, ktorú si tu nenašiel vyriešenú? Pošli nám túto úlohu a my Ti ju skúsime vypočítať. Riešime príklady a úlohy z matematiky. Nielen domáce.
