Stereometria - slovné úlohy a príklady - strana 103 z 119
Počet nájdených príkladov: 2378
- Kocka a kváder
 Určite dĺžku hrany kocky, ktorej objem sa rovná 60% objemu kvádra s rozmermi 7cm, 8cm, 6cm.
Určite dĺžku hrany kocky, ktorej objem sa rovná 60% objemu kvádra s rozmermi 7cm, 8cm, 6cm. - Debničky
 Debničky tvaru kvádra (bez veka) sme sa rozhodli zo všetkých strán (vonkajších i vnútorných) natrieť farbou. Rozmery dna sú 60 cm X 30 cm a výška 12 cm. Koľko plechoviek farby bude treba na natretie 10 takých debničiek, ak jedna plechovka vydrží na natret
Debničky tvaru kvádra (bez veka) sme sa rozhodli zo všetkých strán (vonkajších i vnútorných) natrieť farbou. Rozmery dna sú 60 cm X 30 cm a výška 12 cm. Koľko plechoviek farby bude treba na natretie 10 takých debničiek, ak jedna plechovka vydrží na natret - Koľko 62
 Koľko dm² ozdobného papiera treba na zhotovenie karnevalových čiapok tvaru kužeľa pre 46 prvákov, ak obvod hlavy prváka je 49 cm a výška čiapky má byť 33 cm. Na záhyby je nutné pridať 3 % papiera?
Koľko dm² ozdobného papiera treba na zhotovenie karnevalových čiapok tvaru kužeľa pre 46 prvákov, ak obvod hlavy prváka je 49 cm a výška čiapky má byť 33 cm. Na záhyby je nutné pridať 3 % papiera? - Najväčšia stena
 Určte obsah najväčšej steny hranolu s podstavou obdĺžnika, ktorý má výšku 4 dm, strana c = 5cm a strana b = 6 cm.
Určte obsah najväčšej steny hranolu s podstavou obdĺžnika, ktorý má výšku 4 dm, strana c = 5cm a strana b = 6 cm. - Mlieko v konve
 V nádobe tvare valca je 80 litrov mlieka. Mlieko siaha do výšky 45 cm. Koľko mlieka bude v nádobe, ak bude siahať do výšky 72 cm?
V nádobe tvare valca je 80 litrov mlieka. Mlieko siaha do výšky 45 cm. Koľko mlieka bude v nádobe, ak bude siahať do výšky 72 cm? - Ľadová plocha
 Obdĺžnikové klzisko s rozmermi 55 m a 25 m chceme pokryť vrstvou ľadu hrubou 4 cm. Koľko litrov vody na to potrebujeme, ak voda po zamrznutí zväčší svoj objem o 10%?
Obdĺžnikové klzisko s rozmermi 55 m a 25 m chceme pokryť vrstvou ľadu hrubou 4 cm. Koľko litrov vody na to potrebujeme, ak voda po zamrznutí zväčší svoj objem o 10%? - Na dovolenke
 Ivan a Katka objavili na dovolenke pravidelný ihlan, ktorého podstavou bol štvorec so stranou 230 m a ktorého výška bola rovná polomeru kruhu s rovnakým obsahom ako podstavný štvorec. Katka označila vrcholy štvorca ABCD. Ivan vyznačil na priamke spájajúce
Ivan a Katka objavili na dovolenke pravidelný ihlan, ktorého podstavou bol štvorec so stranou 230 m a ktorého výška bola rovná polomeru kruhu s rovnakým obsahom ako podstavný štvorec. Katka označila vrcholy štvorca ABCD. Ivan vyznačil na priamke spájajúce - Kužeľovitá strecha
 Kužeľovitá strecha nad skladiskom má priemer dolnej časti (podstavy) d = 11,2 m a výšku v = 3, 3m. Koľko oceľových dosiek tvare obdĺžnika s rozmermi 1,4 m a 0,9 m bolo treba na výrobu tejto strechy, ak švami a odpad si vyžiadali zvýšenie ich spotreby o 10
Kužeľovitá strecha nad skladiskom má priemer dolnej časti (podstavy) d = 11,2 m a výšku v = 3, 3m. Koľko oceľových dosiek tvare obdĺžnika s rozmermi 1,4 m a 0,9 m bolo treba na výrobu tejto strechy, ak švami a odpad si vyžiadali zvýšenie ich spotreby o 10 - Karneval
 Žiaci v triede sa dohodli, že na karneval si vyrobia rôzne ozdobné klobúky tvaru kužeľa. Koľko ozdobného materiálu potrebovala trieda s 25 žiakmi na výrobu klobúkov, ak pri vystrihovaní a lepení museli počítať asi s dvadsaťpercentnýn odpadom? ( Rozmery kl
Žiaci v triede sa dohodli, že na karneval si vyrobia rôzne ozdobné klobúky tvaru kužeľa. Koľko ozdobného materiálu potrebovala trieda s 25 žiakmi na výrobu klobúkov, ak pri vystrihovaní a lepení museli počítať asi s dvadsaťpercentnýn odpadom? ( Rozmery kl - Určite 2
 Určite dĺžku hrany kocky, ktorej objem sa rovná 60 % objemu kvádra s rozmermi 7 cm, 8 cm, 6 cm.
Určite dĺžku hrany kocky, ktorej objem sa rovná 60 % objemu kvádra s rozmermi 7 cm, 8 cm, 6 cm. - Povrch kocky - 2
 Vypočítajte, o koľko % sa zmenší povrch kocky, zmenší ak sa dĺžka všetkých hrán o 10%.
Vypočítajte, o koľko % sa zmenší povrch kocky, zmenší ak sa dĺžka všetkých hrán o 10%. - Hranol s kosoštvorcovou
 Nádoba tvaru hranola s kosoštvorcovou podstavou má jednu uhlopriečku podstavy 10cm a hranu podstavy 14cm. Hrana podstavy a výška hranola sú v pomere 2:5. Koľko litrov vody je v nádobe keď je naplnená do štyroch pätín objemu?
Nádoba tvaru hranola s kosoštvorcovou podstavou má jednu uhlopriečku podstavy 10cm a hranu podstavy 14cm. Hrana podstavy a výška hranola sú v pomere 2:5. Koľko litrov vody je v nádobe keď je naplnená do štyroch pätín objemu? - Opísaná a vpísaná
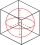 Kocke s objemom 4096cm³ je opísaná a vpísaná guľa. Vypočítajte, koľkokrát je väčší objem opísanej gule ako guľe vpísanej.
Kocke s objemom 4096cm³ je opísaná a vpísaná guľa. Vypočítajte, koľkokrát je väčší objem opísanej gule ako guľe vpísanej. - Kocky - rozdiel
 Hrana druhej kocky je o 2 cm väčšia, než je hrana prvej kocky. Rozdiel objemov kociek je 728 cm³. Vypočítajte veľkosti hrán obidvoch kociek.
Hrana druhej kocky je o 2 cm väčšia, než je hrana prvej kocky. Rozdiel objemov kociek je 728 cm³. Vypočítajte veľkosti hrán obidvoch kociek. - Do kocky 3
 Do kocky K s dĺžkou hrany a je vypísaná guľa G. Do gule G je vypísaná kocka K1. Vypočítaj, koľko percent objemu kocky K tvorí objem kocky K1.
Do kocky K s dĺžkou hrany a je vypísaná guľa G. Do gule G je vypísaná kocka K1. Vypočítaj, koľko percent objemu kocky K tvorí objem kocky K1. - Kúžeľ vo valci
 Do valca je vpísaný kúžeľ. Určite pomer objemu kúžeľa a valca. Pomer vyjadrite ako desatinné číslo a aj ako percento.
Do valca je vpísaný kúžeľ. Určite pomer objemu kúžeľa a valca. Pomer vyjadrite ako desatinné číslo a aj ako percento. - Pomer uhlopriečok
 Dĺžky hrán kvádra sú v pomere 1 : 2 : 3. Budú v takom istom pomere aj dĺžky jeho stenových uhlopriečok? Kváder má rozmery 5 cm, 10 cm a 15 cm. Vypočítaj veľkosť stenových uhlopriečok tohto kvádra.
Dĺžky hrán kvádra sú v pomere 1 : 2 : 3. Budú v takom istom pomere aj dĺžky jeho stenových uhlopriečok? Kváder má rozmery 5 cm, 10 cm a 15 cm. Vypočítaj veľkosť stenových uhlopriečok tohto kvádra. - Sieť valca
 Načrtni sieť valca, ktorého pomer polomeru podstavy k výške je 2 : 3. Vypočítaj objem a povrch valca, ak jeho výška je 9 cm (náčrt, výpočet, odpoveď).
Načrtni sieť valca, ktorého pomer polomeru podstavy k výške je 2 : 3. Vypočítaj objem a povrch valca, ak jeho výška je 9 cm (náčrt, výpočet, odpoveď). - Obklad bazéna
 Vypočítajte koľko metrov štvorcových je potrebných na obklad bazéna dlžky 6 metrov, šírky 4 metre a hlbky 1,5 metra. Prepočítajte 10% na odpad.
Vypočítajte koľko metrov štvorcových je potrebných na obklad bazéna dlžky 6 metrov, šírky 4 metre a hlbky 1,5 metra. Prepočítajte 10% na odpad. - Hranol
 Podstava hranola je kosoštvorec s dĺžkou strany 25 cm a výškou 16 cm. Výška hranola je o 163% väčšia ako dĺžka strany kosoštvorca. Vypočítajte objem hranola.
Podstava hranola je kosoštvorec s dĺžkou strany 25 cm a výškou 16 cm. Výška hranola je o 163% väčšia ako dĺžka strany kosoštvorca. Vypočítajte objem hranola.
Máš príklad, ktorý si tu nenašiel vyriešenú? Pošli nám príklad a my Ti ho skúsime vypočítať.
