Trojuholník
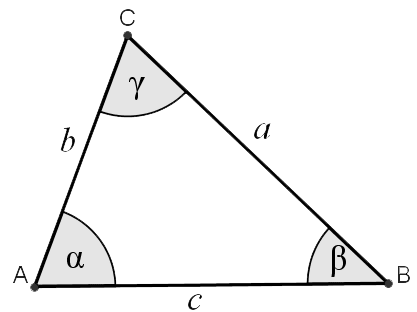
Kalkulačka rieši trojuholník zadaný troma jeho vlastnosťami. Každý trojuholník má šesť hlavných vlastností - tri strany a, b, c (dĺžky strán) a tri uhly (α, β, γ). Klasická trigonometrická úloha je zo zadaných troch vlastností dopočítať zvyšné tri. Naša kalkulačka samozrejme rieši trojuholníky zo zadaných ľubovoľných kombinácií hlavných a aj odvodených vlastností, ako sú napr. plocha, obvod, výsky, ťažnice. Zvyčajne troma stranami (sss), strana-uhol-strana, uhol-strana-uhol.
Ako vypočíta (vyrieši) táto trojuholníkova kalkulačka trojuholník?
Výpočet obecného trojuholníka má dve fázy:- expertná fáza - ktorá je rôzna pre rôzne zadané úlohy. Zo zadaných údajov sa kalkulačna snaží vypočítať veľkosti troch strán trojuholníka. Na zadané údaje postupne aplikuje bázu znalostí, ktorú predstavujú najmä vzťahy medzi jednotlivými parametrami trojuholníka.
Tie sa postupne vhodne aplikujú a kombinujú a vypočítavajú sa ďaľšie a ďaľšie parametre trojuholníka. Toto sa iteruje až kým trojuholník ma vypočítané všetky tri strany.
Napríklad z daného obsahu trojuholníka a príslušnej strany, dopočíta sa príslušná výška. Zo známej výšky a uhla sa môže dopočítať priľahlá strana atď. Používajú sa znalostí napr. vzorce (vzťahy) Pytagorova veta, sínusová veta, kosínusova veta, Herónov vzorec, riešia rovnice a sústavy rovníc. - druhá fáza je dopočet vlastností trojuholníka zo známych dĺžok troch jeho strán
Príklady ako zadať trojuholník:
a=3 b=4 c=5 ... výpočet trojuholníka z troch strán a,b,c.
B=45 c=10 a=9 ... výpočet trojuholníka z dvoch strán a,c a nimi zovretého uhla B.
A=25 C=80 b=22
A=35 C=26 a=10
a=3 C=90 c=5 ... ako vložiť pravouhlý trojuholník.
a=3 β=25 γ=45 ... trojuholník - výpočet, ak viem stranu a dva uhly.
a=3 β=25 S=12 ... trojuholník - výpočet, ak viem stranu, uhol a plochu trojuholníka.
S=2.5 c=2 b=4 ... nájdi stranu a ak viem strany b,c a plochu trojuholníka S.
ta=1 b=2.5 c=2 ... výpočet trojuholníka, ak viem jednu tažnicu a dve ľubovoľné strany.
ta=1 tb=2.5 tc=2 ... výpočet trojuholníka z ťažníc.
va=220, vb=165 vc=132 ... výpočet trojuholníka ak sú známe tri výšky.
a=7 β=40 tc=5 ... výpočet trojuholníka ak je známa strana, uhol, ťažnica.
a:b:c=2:3:4 S=2.5 ... výpočet trojuholníka ak je známy pomer strán a obsah.
A:B:C=1:4:5 a=2 ... výpočet trojuholníka ak je známy pomer vnútorných uhlov a jedna strana.
B=45 c=10 a=9 ... výpočet trojuholníka z dvoch strán a,c a nimi zovretého uhla B.
A=25 C=80 b=22
A=35 C=26 a=10
a=3 C=90 c=5 ... ako vložiť pravouhlý trojuholník.
a=3 β=25 γ=45 ... trojuholník - výpočet, ak viem stranu a dva uhly.
a=3 β=25 S=12 ... trojuholník - výpočet, ak viem stranu, uhol a plochu trojuholníka.
S=2.5 c=2 b=4 ... nájdi stranu a ak viem strany b,c a plochu trojuholníka S.
ta=1 b=2.5 c=2 ... výpočet trojuholníka, ak viem jednu tažnicu a dve ľubovoľné strany.
ta=1 tb=2.5 tc=2 ... výpočet trojuholníka z ťažníc.
va=220, vb=165 vc=132 ... výpočet trojuholníka ak sú známe tri výšky.
a=7 β=40 tc=5 ... výpočet trojuholníka ak je známa strana, uhol, ťažnica.
a:b:c=2:3:4 S=2.5 ... výpočet trojuholníka ak je známy pomer strán a obsah.
A:B:C=1:4:5 a=2 ... výpočet trojuholníka ak je známy pomer vnútorných uhlov a jedna strana.
Čo znamenajú symboly?
a, b, c ... strany BC, AC, AB
A, B, C alebo α, β, γ ... vnútorné uhly
va, vb, vc ... výšky
ta, tb, tc ... ťažnice
S ... obsah
o ... obvod
s ... semiperimeter (poloobvod)
Trojuholníky v slovných úlohách:
- Šípka-vpravo súradnice
Trojuholník má vrcholy na (4, 5), (-3, 2) a (-2, 5). Aké sú súradnice vrcholov obrazu po preložení (x, y) šípka-vpravo (x + 3, y - 5)? - Vonkajšie uhly
ABC trojuholnik, alfa = 54stupňov 32 minút, beta = 79 stupňov. Aké sú veľkosti vonkajšich uhlov? - Strany trojuholníka 2
zmeň trojuholník v pomere 3:4 strany trojuholníka : a = 7 cm b = 6 cm c = 5 cm - Strany 7
Strany trojuholníka sú 5,2, 4,6 a x. Ak je OBVOD trojuholníka 11,2 stôp, aká je dĺžka neznámej strany? (nápoveda: nakreslite obrázok) - Okolo 7
Okolo záhonu tvaru trojuholníka so stranami 5 m, 6 m a 10 m záhradnik sadí jeden rád tulipánov. Koľko cibuliek tulipánov potrebuje, ak na dĺžku 1 m chce zasadiť 8 cibuliek? - Narysuj 17
Narysuj ľubovoľný trojuholník. Zostroj osi jeho dvoch strán. Ich priesečník je bod S. a) Odmeraj vzdialenosť bodu S od všetkých troch vrcholov- b) Dorysuj os tretej strany. - Rovnoramenný 2
Rovnoramenný trojuholníkový rám má ramená dlhé 72 metrov a základňu 18 metrov. Nájdite obvod rámu. - Uhol
Narysuj uhol |∠ ABC| = 130° a zostroj jeho os. Akú veľkosť má uhol, ktorý zviera os uhla s ramenom uhla? - Trojúholník ABC
Zostroj trojuholník ABC ak platí c = 60 mm Vc = 40 mm b = 48 mm rozbor postup konštrukcia - Pravouhlý 26
Pravouhlý trojuholník ABC má preponu c dlhú 9 cm a časť prepony cb= 3 cm. Aká dlhá je výška na stranu c? - Cvičenci 3
Cvičenci stoja na značkách v radoch vzdialených od seba presne 1,5 m. Tvoria rozširujúci sa trojuholníkový klin (v každom nasledujúcom rade je o jedného cvičenca viac), pričom vzdialenosť čelného cvičenca od zadného radu je 30 m. Určte počet cvičencov. - V trojuholníku 2
V trojuholníku XYZ, ak meria uhol X=40° a meria uhol Y=75°. Ktorá strana trojuholníka je najdlhšia a prečo? - Trojuholník - PT - uhol V pravouhlom trojuholníku je veľkosť uhla 40°. Nájdite veľkosť ostatných uhlov trojuholníka v stupňoch.
- Rovnoramenný trojuholník 4
Obvod trojuholnika s dvoma rovnakymi stranami je 117 cm. Tretia strana meria 44 cm. Koľko cm meria jedna zo zvyšných strán? - Horná hranica
Strany rovnostranného trojuholníka sú dlhé 9,4 cm s presnosťou na jedno desatinné miesto. Vypočítajte hornú hranicu strany tohto trojuholníka.
slovné úlohy - viacej »
