Zlomkový kalkulátor

Pravidla výrazů se zlomky:

Znak / je zlomková čára, případně znak dělení - napr. 5/100 nebo 1/2 / 3.
Smíšené číslo se skládá z celé části a zlomkové části. Zapisujeme jako celé číslo mezera zlomek. Smíšené číslo (smíšený zlomek) se zapíše např. 1 2/3 (jedna a dvě třetiny).
Desetinná čísla se píší s desetinnou tečkou . nebo čárkou , a automaticky se převedou na zlomky - napr. 1,45.

Dvojtečka : znamená dělení, například na dělení smíšených čísel: 1 2/3 : 4 3/8.
Hvězdička * znamená násobení.
Plus + je sčítání, mínus - je odčítání, () {} [] jsou závorky.
Znak umocnění je ^ - použití například: 1/4^3

Příklady použití:

• sčítání zlomků: 2/4 + 3/4
• odčítání zlomků: 2/3 - 1/2
• násobení zlomků: 7/8 * 3/9
• dělení zlomků: 1/2 : 3/4
• převrácený zlomek: 1 : 3/4
• druhá mocnina zlomku: 2/3 ^ 2
• třetí mocnina zlomku: 2/3 ^ 3
• umocnění zlomků: 1/2 ^ 4
• umocnění na zlomek: 16 ^ 1/2
• sčítání zlomků a smíšených čísel: 8/5 + 6 2/7
• dělení celého čísla a zlomků: 5 ÷ 1/2
• složený zlomek: 5/8 : 2 2/3
• číslo na zlomek: 0.625
• zlomek na desetinné číslo: 1/4
• zlomek na procenta: 1/8 %
• porovnávaní zlomků: 1/4 2/3
• odmocnina ze zlomku: sqrt(1/16)
• výraz se závorkami: 1/3 * (1/2 - 3 3/8)
• zlomek ze zlomku: 3/4 z 5/7
• násobení: 2/3 z 3/5
• dělením najděte kvocient: 3/5÷2/3

Understanding Order of Operations

Ever wondered why calculators don't just work left to right? This calculator follows the mathematical order of operations — a set of rules that ensures everyone solves expressions the same way, every time.

Popular Memory Tricks

Different regions use different mnemonics to remember this order:

* PEMDAS - Parentheses, Exponents, Multiplication, Division, Addition, Subtraction
* BEDMAS - Brackets, Exponents, Division, Multiplication, Addition, Subtraction
* BODMAS - Brackets, Order (or "Of"), Division, Multiplication, Addition, Subtraction
* GEMDAS - Grouping symbols (parentheses, brackets, braces: (){}), Exponents, Multiplication, Division, Addition, Subtraction

The Golden Rules

Rule 1: Multiplication and division always come before addition and subtraction. Think of them as the VIPs that skip to the front of the line!

Rule 2: When operations have equal priority (like × and ÷, or + and −), work from left to right—just like reading a book.

Pro tip: MDAS is a simplified version focusing on the core concept: Multiplication and Division share the same priority level, as do Addition and Subtraction.

Zlomky v slovních úlohách:

• Šestiny z miliónu
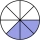  Prosím kolik je 2/6 z 10,000,000,-Kč?
• Zubní kazy
  7. B třída je na preventivní zubní prohlídce. Čtvrtině žáků zjistili dva zubní kazy, osmině jeden kaz. Polovina třídy měla všechny zuby zdravé. Kolik žáků chodí do 7. B, pokud v den zubní prohlídky tři žáci chyběli?
• Hrušky
  V košíku byly hrušky, vzal jsem z nich dvě pětiny a zůstalo jejich v košíku šest. Kolik hrušek jsem vzal?
• Rovnice se zlomky
  Nájdite hodnotu y: 3/5y-9/4 (y +4)-1=1/2 (3y-2)-3(3-y)
• Součet zlomků
  Najděte součet, vyjádřete svou odpověď na nejnižší výrazy. 1. 1/4 + 2/4 = 2. 1/6 + 3/6= 3. 6/10 + 2/10= 4, ¾ + ⅛= 5, 5 3/5 + 2 ½ =
• Hodnota x z rovnice
  Najděte hodnotu x: x/5+x/2=-1/5-3x/2
• Nepravé zlomky
  Jak identifikovat nepravé zlomky? Které z následujících zlomků jsou nepravé? A) 3/4 B) 32/15 C) 3/9 D) 2 2/11

slovní úlohy - více »