Pravidelný trojboký
Pravidelný trojboký hranol, jehož hrany jsou shodné, má povrch 2514 cm2 (čtverečních). Urči objem tohoto tělesa v cm3 (l).
Správná odpověď:
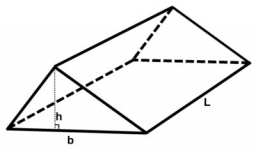
Tipy na související online kalkulačky
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Pythagorova věta je základ výpočtů kalkulačky pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Pythagorova věta je základ výpočtů kalkulačky pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebrastereometrieplanimetrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Související a podobné příklady:
- Čtyřstěn 3
Pravidelný čtyřstěn je trojboký jehlan, jehož podstava a stěny jsou shodné rovnostranné trojúhelníky. Vypočítejte výšku tohoto tělesa, je-li délka hrany a = 8 cm - Trojboký hranol
Pravidelný trojboký hranol je vysoký 7 cm. Jeho podstava je rovnostranný trojúhelník, jehož výška je 3 cm. Vypočítejte povrch a objem tohoto hranolu. - Trojboký hranol 16
Vypočítejte povrch pravidelného trojbokého hranolu, jehož hrany podstavy mají délku 6 cm a výška hranolu je 15 cm . - Osmistěn
Všechny stěny pravidelného osmistěn jsou shodně rovnostranné trojúhelníky. Hrany osmistěnu ABCDEF mají délku d = 6 cm. Vypočtěte povrch a objem tohoto osmistěnu. - Povrch a objem
Vypočítejte povrch a objem válce jehož výška je 8 dm a poloměr kružnice podstavy je 2 dm - Pravidelný 11
Pravidelný trojboký jehlan ABCDV má délku podstavné hrany a=8 cm a výšku 7 cm. Vypočítej povrch a objem jehlanu - Trojboký hranol
Vypočítejte objem pravidelného trojbokého hranolu, jehož výška je rovna délce podstavné hrany. Objem vypočítejte pro délku hrany a = 6 cm.
