Čtvercova sít
Čtvercova síť se skladá ze čtverců se stranou délky 1 cm. Narysujte do ní alespoň tři různe obrazce takové, aby každý měl obsah 6 cm2 a obvod 12 cm a aby jejich strany splývaly s přímkami síťe.
Vaše odpověď:
Vaše odpověď:
Zobrazuji 2 komentáře:
Mo-radce
Nápověda. Načrtněte si nějaký útvar s obsahem 6 cm2 a upravujte jej tak, aby byly splněny ostatní podmínky.
Možné řešení. Jednoduchým útvarem s obsahem 6 cm2 je např. obdélník se stranami délek 2 cm a 3 cm. Ten má však obvod pouze 10 cm; potřebujeme přesunout část jeho plochy tak, aby se obvod o 2 cm zvětšil. To si lze v rámci zadané čtvercové sítě představit tak, že zkoušíme přesouvat jednotlivé čtverce obsažené v obdélníku na jiná místa. Několik možných řešení je na obrázku:
110
111
001
110
111
010
0110
1111
Poznámka. Zvídavější řešitel se může zamyslet nad dalšími, příp. všemi možnými řešeními. K tomu si stačí povšimnout, že při přesouvání dílčích čtverců myšleného obdélníku se obvod zvětší buď o 2 cm, nebo o 4 cm, a to podle toho, zda je tento čtverec rohový, nebo ne.
Možné řešení. Jednoduchým útvarem s obsahem 6 cm2 je např. obdélník se stranami délek 2 cm a 3 cm. Ten má však obvod pouze 10 cm; potřebujeme přesunout část jeho plochy tak, aby se obvod o 2 cm zvětšil. To si lze v rámci zadané čtvercové sítě představit tak, že zkoušíme přesouvat jednotlivé čtverce obsažené v obdélníku na jiná místa. Několik možných řešení je na obrázku:
110
111
001
110
111
010
0110
1111
Poznámka. Zvídavější řešitel se může zamyslet nad dalšími, příp. všemi možnými řešeními. K tomu si stačí povšimnout, že při přesouvání dílčích čtverců myšleného obdélníku se obvod zvětší buď o 2 cm, nebo o 4 cm, a to podle toho, zda je tento čtverec rohový, nebo ne.
Tipy na související online kalkulačky
Hledáte pomoc s výpočtem kořenů kvadratické rovnice?
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebraplanimetrietémaÚroveň náročnosti úkolu
Související a podobné příklady:
- Čtvercová síť
Narýsuj čtverec tak aby jeho strany neležely na čarách čtvercové sítě - Konstrukce obdélníku
Na obrázku je čtvercová síť ve které má strana jednoho čtverce délku 1 cm. Narýsuj obdélník o obsahu 18 čtverců, který má obvod 22 cm. - Jazyky na recepci
Na recepci na velvyslanectví každý ovládá alespoň jeden cizí jazyk: 15 lidí mluví anglicky 12 lidí mluví německy 7 oběma Z kolika lidí se skládá tato společnost, pokud v ní nikdo nemluví jiným jazykem? - Obrazec
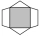Obrazec se skládá z tmavého čtverce, dvou shodných bílých rovnoramenných trojúhelníků a dvou shodných bílých lichoběžníků. (S každou stranou čtverce splývá základna jednoho bílého útvaru. ) Tmavý čtverec má stranu délky 12 cm a jeho obsah je polovinou obs - Skladovací prostor
Frank navrhl síť pro skladovací prostor, který se chystá postavit z kovu. Design se skládá ze čtvercové základny a čtyř čtverečních stran plus čtyř trojúhelníkových částí, které tvoří střechu. Čtvercová základna 6 stop a čtyři čtvercové strany plus 4 stop - Načrtni
Načrtni sít kužele a připiš k ní délku strany, délku oblouku kružnice a délku kružnice, když znáš: délku strany kužele: s = 51,9 cm obvod podstavy kužele= O =151 mm. - Obvod půdorysu stánků
Půdorys prodejních stánků se skládá ze čtverců a ve skutečnosti má obsah 48 m². Jaký obvod má půdorys těchto stánků? a. 34 m b. 36 m c. 40 m d. 44 m
