Lichoběžník - 4 strany
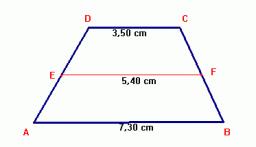
V lichoběžníku ABCD je |AB|=73,6 mm; |BC|=57 mm; |CD| =60 mm; |AD|=58,6 mm. Vypočítejte velikosti jeho vnitřních úhlů.
Vaše odpověď:
Vaše odpověď:
Zobrazuji 1 komentář:
Tipy na související online kalkulačky
Kosinovú větu přímo používá kalkulačka SUS trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
planimetriezákladní operace a pojmygoniometrie a trigonometrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Související a podobné příklady:
- Úhly trojúhelníku v lichoběžníku
Daný je rovnoramenný lichoběžník ABCD, ve kterém platí |AB|= 2|BC|= 2|CD|= 2|DA|. Na jeho straně BC je bod K takový, že |BK| = 2|KC|, na jeho straně CD je bod L takový, že |CL|= 2|LD|, a na jeho straně DA je bod M takový, že |DM|= 2|MA|. Určete velikosti - V lichoběžníku 5
V lichoběžníku ABCD (AB II CD) je α = 57°, γ = 4β. Vypočítejte velikost všech vnitřních úhlů. - V rovnoramenný lichoběžník
V rovnoramenném lichoběžníku ABCD jsou dány jeho základny AB=20 cm, CD=12 cm a ramena AD=BC=8 cm. Určete jeho výšku a úhel alfa při vrcholu A. - Rovnoramenný lichoběžník
Je dán rovnoramenný lichoběžník ABCD, v němž platí: |AB| = 2|BC| = 2|CD| = 2|DA|: Na jeho straně BC je bod K takový, že |BK| = 2|KC|, na jeho straně CD je bod L takový, že |CL| = 2|LD|, a na jeho straně DA je bod M takový, že |DM| = 2|MA|. Určete velikost - Čtyřboký hranol 6
Vypočítej povrch čtyřbokého hranolu ABCDA'B'C'D' s lichoběžníkovou podstavou ABCD. Výška hranolu je 12 cm; údaje o lichoběžníku ABCD: délka základny AB je 8 cm, délka základny CD je 3 cm, délka ramene BC je 4 cm a délka úhlopříčky AC je 7 cm. Napovíme: Na - Plavecký
Plavecký bazén dlouhý 30 metrů je naplněn vodou do hloubky 1 metru na mělkém konci a 5 metrů na hlubokém konci a svislé ploše bazénu má tvar lichoběžníku s plochou danou S (abcd). = 1/2 (ab + cd) x ad. Jaká je plocha průřezu abcd? - Obvod lichoběžníku
Je dán lichoběžník ABCD (AB||CD, AB kolmé na AD). Vypočti jeho obvod, pokud |AB|=20 cm, |CD|=15 cm, |AD|=12 cm. Pythagorova věta
