Ramena lichoběžníku

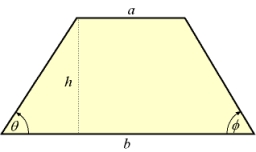
Vypočtená délku ramen v rovnoramenném lichoběžníku. Výsledek zaokrouhlí na 2 desetinná místa. Úhlopříčka alfa se rovná 0,4 m a úhlopříčka beta se rovná 0,4 m. Strana AB má 120 cm a strana DC má 7,6 dm.

Správná odpověď:

r =  102,3719 cm

Postup správného řešení:

$$\begin{gathered} u=1,4\text{m}\to \text{cm}=1,4\cdot 100\text{cm}=140\text{cm} \\ a=120\text{cm} \\ c=7,6\text{dm}\to \text{cm}=7,6\cdot 10\text{cm}=76\text{cm} \\ x=(a-c)/2=(120-76)/2=22\text{cm} \\ h=\sqrt{u^2-(c+x{)}^2}=\sqrt{140^2-(76+22{)}^2}=14\sqrt{51}\text{cm}\doteq 99,98\text{cm} \\ r=\sqrt{h^2+x^2}=\sqrt{99,98^2+22^2}=4\sqrt{655}=102,3719\text{cm} \end{gathered}$$

Zkusit jiný příklad