Pythagorova věta - slovní úlohy a příklady - strana 42 z 73
Počet nalezených příkladů: 1444
- V rovině 2
V rovině je umístěn trojúhelník ABC s pravým úhlem u vrcholu C, pro který platí: A(1, 2), B(5, 2), C(x, x+1), kde x > -1. a) určete hodnotu x b) určete souřadnice bodu M, který je středem úsečky AB c) dokažte že vektory AB a CM jsou kolmé d) určete vel - Parašutista
Po otevření padáku klesá výsadkář k zemi stálou rychlostí 2 m/s, přičemž ho unáší boční vítr stálou rychlostí 1,5 m/s. Určete: a) velikost jeho výsledné rychlosti vzhledem k zemi, b) vzdálenost místa jeho dopadu od osamělého stromu, nad nímž se nacházel v - Navigace lodě
Loď pluje 84 km na kurzu 17° a pak cestuje na kurzu 107° 135 km. Najděte vzdálenost konce cesty z výchozího bodu a zaokrouhlete je na nejbližší kilometr. - Z=-√2-√2i 74744
Nechť komplexní číslo z=-√2-√2i, kde i² = -1. Najděte |z|, arg(z), z* (kde * označuje komplexní konjugát) a (1/z). V případě potřeby napište své odpovědi ve tvaru a + i b, kde ai b jsou reálná čísla. Označte polohy čísel z, z* a (1/z) na Argandově diagram - Násep
Na vodorovné rovině má být vybudován násep vysoký 7,5m, šířka horní plochy náspu je 2,9 m, sklon svahu je 35°. Jaká bude dolní šířka náspu? - Pravoúhly trojúhelník 9
V pravoúhlém trojúhelníku ABC s pravým úhlem při vrcholu C je dáno : a=17cm, Vc=8 cm. Vypočítejte délku stran b, c, jeho obsah S, obvod o, délku poloměrů kružnic trojúhelníku opsané R a vepsané r a velikost úhlů alfa a beta. - Úhel mezi vektory
Najděte úhel mezi danými vektory a zaokrouhlete výsledek na desetinu stupně. u = (1, 9) a v = (-14, 14) - Pravoúhlý trojúhelník
Pro odvěsny pravoúhlého trojúhelníku platí a:b = 7:8. Přepona má délku 88 cm. Vypočítejte obvod a obsah tohoto trojúhelníku. - Koza
Ve čtvercové zahradě o straně (a), je uprostřed jedné strany uvázaná koza. Spočítej délku provazu (r) tak, aby koza spásla přesně půlku zahrady. Platí r=c*a, urči konstantu c. - Záhon 10
Záhon tvaru dvou rovnostranných trojúhelníků se společnou stranou, s délkou strany 2,5 m má být osázen sazenicemi okrasného keře. Zahradník doporučil mezi jednotlivými sazenicemi ponechat mezery 40 cm a na samotnou sazenici je potřeba 10 cm z obvodu. Urči - Pravoúhlý lichoběžník 6
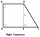Pravoúhlý lichoběžník ABCD se základnami AB a CD je rozdělen úhlopříčkou AC na dva rovnoramenné pravoúhlé trojúhelníky. Délka úhlopříčky AC je rovna 62 cm. Vypočítejte v cm čtverečných obsah lichoběžníku a vypočítej, o kolik cm se liší obvody trojúhelníků - Vzdálenosti 6653
Dvě přímé cesty se křižují a svírají úhel alfa = 53 stupňů 30'. Na jedné z nich stojí dva sloupy, jeden na křižovatce, druhý ve vzdálenosti 500m od ní. Jak daleko je třeba jít od křižovatky po druhé cestě, abychom viděli oba sloupy v zorném úhlu beta? a) - Nepřístupne místa
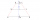Určete vzdálenost dvou nepřístupných míst P, Q, pokud vzdálenost dvou pozorovacích míst A, B je 2000m a znáte-li velikost úhlů QAB = 52°40'; PBA = 42°01'; PAB = 86°40' a QBA = 81°15'. Uvažovaná místa A, B, P, Q leží v jedné rovině. - Vypočítejte: 8173
Polohový vektor hmotného bodu, který se pohybuje v rovině, je možné v zavedené vztažné soustavě vyjádřit vztahem: r(t) = (2t + 3t²; 6t + 3), kde t je čas v sekundách a souřadnice vektoru jsou v metrech. Vypočítejte: a) jaká je poloha hmotného bodu v době - Dvě silnice
Dvě silnice spolu svírají pravý úhel. Na jedné silnici je 5km od křižovatky místo P, na druhé silnici je 12km od křižovatky místo R. Místa P a R jsou spojena přímou pěšinou. Chodec jde z místa R do místa P pěšinou průměrnou rychlostí 5km/h, auto jede z mí - V pravoúhlém 8
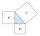V pravoúhlém trojúhelníku ABC (AB je přepona) platí a : b = 24 : 7 a výška na stranu c = 12,6 cm. Vypočítejte délky stran trojúhelníku ABC. - Vypočítejte
Vypočítejte délku tětivy v kružnici o poloměru 25 cm, které přísluší obvodový úhel 26°. - Čtvrtkruh
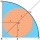Jaký poloměr má kruh vepsaný do čtvrtkruhu o poloměru 100 cm? - Sestrojený čtverce Na dvěma stranami trojúhelníku ABC jsou sestrojeny čtverce. Obsah čtverce nad stranou BC je 25 cm². Velikost výšky vc na stranu AB je 3 cm. Pata P výšky vc dělí stranu AB v poměru 2 : 1. Strana AC je delší než strana BC. Vypočtěte v cm délku strany AB. Vy
- Vypočítejte: 8174 Polohový vektor hmotného bodu, který se pohybuje v rovině, lze v zavedené vztažné soustavě vyjádřit vztahem: r(t) = (1 + 5t + 2t² ; 3t + 1), kde t je čas v sekundách a souřadnice vektoru jsou v metrech. Vypočítejte: a) jaká je poloha hmotného bodu v době
Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
