Příklady na tětiva - strana 2 z 4
Pamatujte: Každý problém vyřešte promyšleně a nezapomeňte pro každou otázku ukázat kompletní řešení.Počet nalezených příkladů: 74
- Tětiva
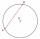 Strana trojúhelníku vepsaného do kružnice je tětivou procházející jejím středem. Jakou velikost mají vnitřní úhly trojúhelníku, pokud jeden z nich má 40°?
Strana trojúhelníku vepsaného do kružnice je tětivou procházející jejím středem. Jakou velikost mají vnitřní úhly trojúhelníku, pokud jeden z nich má 40°? - Dvě tětivy
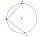 Je dána kružnice k (S, r). Z bodu A který patří k jdou dvě tětivy s délkou r. Jaký úhel svírají? Narysuj a odměř.
Je dána kružnice k (S, r). Z bodu A který patří k jdou dvě tětivy s délkou r. Jaký úhel svírají? Narysuj a odměř. - Rovnoběžné tětivy
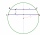 V kružnici s průměrem 70 cm jsou narýsované dvě rovnoběžné tětivy tak, že střed kružnice leží mezi tětivami. Vypočítejte vzdálenost těchto tětiv, pokud jedna z nich má délku 42 cm a druhá 56 cm.
V kružnici s průměrem 70 cm jsou narýsované dvě rovnoběžné tětivy tak, že střed kružnice leží mezi tětivami. Vypočítejte vzdálenost těchto tětiv, pokud jedna z nich má délku 42 cm a druhá 56 cm. - Rovnoběžné tětivy
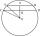 V kružnici s r = 26 cm jsou narýsované 2 rovnoběžné tětivy. Jedna tětiva má délku t1 = 48 cm a druhá má délku t2 = 20cm, přičemž střed leží mezi nimi. Vypočítejte vzdálenost dvou tětiv.
V kružnici s r = 26 cm jsou narýsované 2 rovnoběžné tětivy. Jedna tětiva má délku t1 = 48 cm a druhá má délku t2 = 20cm, přičemž střed leží mezi nimi. Vypočítejte vzdálenost dvou tětiv. - Tětiva
 Jakou délku x má tětiva kružnice o průměru 120 km, pokud je vzdálena od středu kružnice 14 km?
Jakou délku x má tětiva kružnice o průměru 120 km, pokud je vzdálena od středu kružnice 14 km? - Tetiva
 Bod na kružnici je krajním bodem průměru a tětivy velikosti poloměru. Jaký úhel svírá průměr s tětivou?
Bod na kružnici je krajním bodem průměru a tětivy velikosti poloměru. Jaký úhel svírá průměr s tětivou? - Je dána 4
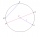 Je dána kružnice o poloměru 10 cm a její tětiva, která má délku 12 cm. Vypočtěte velikost středového úhlu, který této tětivě přísluší.
Je dána kružnice o poloměru 10 cm a její tětiva, která má délku 12 cm. Vypočtěte velikost středového úhlu, který této tětivě přísluší. - Dve tětivy
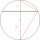 Vypočítejte délku tětivy AB a k ní kolmé tětivy BC, pokud tětiva AB je od středu kružnice k vzdálená 4 cm a tětiva BC má vzdálenost 8 cm.
Vypočítejte délku tětivy AB a k ní kolmé tětivy BC, pokud tětiva AB je od středu kružnice k vzdálená 4 cm a tětiva BC má vzdálenost 8 cm. - V kružnici
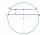 V kružnici o poloměru 8,5 cm jsou sestrojeny dvě rovnoběžné tětivy, jejichž délky jsou 9 cm a 12 cm. Vypočítejte vzdálenost tětiv v kružnici.
V kružnici o poloměru 8,5 cm jsou sestrojeny dvě rovnoběžné tětivy, jejichž délky jsou 9 cm a 12 cm. Vypočítejte vzdálenost tětiv v kružnici. - Z9–I–3
 Julince se zakutálel míček do bazénu a plaval ve vodě. Jeho nejvyšší bod byl 2 cm nad hladinou. Průměr kružnice, kterou vyznačila hladina vody na povrchu míčku, byl 8 cm. Určete průměr Julinčina míčku.
Julince se zakutálel míček do bazénu a plaval ve vodě. Jeho nejvyšší bod byl 2 cm nad hladinou. Průměr kružnice, kterou vyznačila hladina vody na povrchu míčku, byl 8 cm. Určete průměr Julinčina míčku. - Rovnice kružnice
 Najděte rovnici kružnice, která se dotýká osy y ve vzdálenosti 4 od počátku a vysekne tětivu délky 6 na ose x.
Najděte rovnici kružnice, která se dotýká osy y ve vzdálenosti 4 od počátku a vysekne tětivu délky 6 na ose x. - Tětiva 4
 Potřebuji vypočítat obvod kruhu, když znám délku tětivy t=26 cm a vzdálenost ode středu d=13 cm tětivy ke kružnici.
Potřebuji vypočítat obvod kruhu, když znám délku tětivy t=26 cm a vzdálenost ode středu d=13 cm tětivy ke kružnici. - Tětiva
 V kružnici o poloměru r = 70 cm je tětiva 10 × delší než její vzdálenost od středu. Jaká je délka tětivy?
V kružnici o poloměru r = 70 cm je tětiva 10 × delší než její vzdálenost od středu. Jaká je délka tětivy? - Tětiva AB
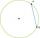 Jakou délku má tětiva AB, jejíž vzdálenost od středu S kružnice k (S, 20 cm) se rovná 10 cm?
Jakou délku má tětiva AB, jejíž vzdálenost od středu S kružnice k (S, 20 cm) se rovná 10 cm? - Tětiva 20
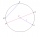 V kružnici s průměrem d= 10 cm, je sestrojena tětiva o délce 6 cm. Jaký poloměr by měla soustředná kružnice, která by se této tětivy dotýkala?
V kružnici s průměrem d= 10 cm, je sestrojena tětiva o délce 6 cm. Jaký poloměr by měla soustředná kružnice, která by se této tětivy dotýkala? - Chodník jak tětiva
 Vypočítej délku chodníku, který vede přes kruhové náměstí s průměrem 40 m, pokud je chodník od středu náměstí vzdálen 15 m
Vypočítej délku chodníku, který vede přes kruhové náměstí s průměrem 40 m, pokud je chodník od středu náměstí vzdálen 15 m - Určete 4
 Určete vzdálenost dvou rovnoběžných tětiv délek 7 cm a 11 cm v kružnici s poloměrem 7 cm
Určete vzdálenost dvou rovnoběžných tětiv délek 7 cm a 11 cm v kružnici s poloměrem 7 cm - Tětiva
 Jakou vzdálenost mají tečna t kružnice (S, 4 cm) a tětiva této kružnice, která má délku 6 cm a je rovnoběžná s tečnou?
Jakou vzdálenost mají tečna t kružnice (S, 4 cm) a tětiva této kružnice, která má délku 6 cm a je rovnoběžná s tečnou? - Tětiva kružnice
 Vypočítejte délku tětivy kružnice o poloměru r = 10 cm, jejíž délka se rovná její vzdálenosti od středu kružnice.
Vypočítejte délku tětivy kružnice o poloměru r = 10 cm, jejíž délka se rovná její vzdálenosti od středu kružnice. - Tětiva 16
 Je dána kružnice k(S, r=6cm) a na ní body A, B tak, že /AB/ = 8cm. Vypočítej vzdálenost středu S kružnice k od středu C úsečky AB.
Je dána kružnice k(S, r=6cm) a na ní body A, B tak, že /AB/ = 8cm. Vypočítej vzdálenost středu S kružnice k od středu C úsečky AB.
Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
