Úhlopříčka + pravoúhlý trojúhelník - příklady a úlohy - strana 12 z 18
Počet nalezených příkladů: 345
- Kvádr
Kvádr má objem 40 cm³. Kvádr má celkovou plochu 100 cm čtverečních. Jedna hrana kostky má délku 2 cm. Najděte délku úhlopříčky kvádru. Dejte svou odpověď správně na 3 desetinná místa. - Jehlan 6
Vypočítej povrch a objem pravidelného čtyřbokého komolého jehlanu : a1= 18 cm , a2=6cm /úhel alfa/α=60° (Úhel α je úhel mezi boční stěnou a rovinou podstavy.) S=? , V=? - Špejle
Sklenice má tvar válce s vnitřním průměrem 12 cm, výška sklenice ode dna je 16 cm. Seříznutou špejli lze šikmo vložit do sklenice tak, že nepřečnívá přes okraj. Jaká je největší možná délka seříznuté špejle? (Tloušťka špejle se při výpočtu zanedbává.) - Úhlopříčka 15
Vypočítejte objem krychle, jejíž tělesová úhlopříčka má velikost 75 dm. Načrtněte si obrázek a tělesovou úhlopříčku barevně zvýrazněte. - Vypočítej 39
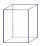Vypočítej objem (V) a povrch (S) pravidelného čtyřbokého hranolu, jehož výška je 28,6 cm a odchylka tělesové úhlopříčky od roviny podlahy je 50°. - Truhlář
Kvádr s podstavou a rozměry 12 cm a 5 cm a výšce 4 cm. Truhlář tento kvádr rozřezal na dva shodné trojboké hranoly s podstavami ve tvaru pravoúhlého trojúhelníku. Truhlář vytvořeny hranoly natřel barvou. Vypočítejte povrch jednoho z těchto dvou trojbokých - Roviny bočních stěn
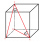Vypočítej objem a povrch kvádru jehož strana c má délku 30 cm a tělesová úhlopříčka svírá s rovinami bočních stěn úhly o velikostech 24 st. 20’, 45 st. 30’ - Hranol 4b-pravidelný
Vypočítejte objem a povrch pravidelného čtyřbokého hranolu jehož výška je 28,6cm a tělesová úhlopříčka svírá s rovinou podstavy úhel 50 stupnů. - Šestihran
Pravidelný šestihran (6 úhelník) se stěnou 6 cm je otočen o 60 ° podél přímky procházející její nejdelší úhlopříčce. Jaký je objem takto vytvořeného tělesa? - Tělesová
Tělesová úhlopříčka pravidelného čtyřbokého hranolu svírá s podstavou úhel velikosti 60°. Hrana podstavy má délku 10cm. Vypočítejte objem tělesa. - Koule 24
V krychli je naskládáno 9 shodných koulí a to tak, aby co nejvíce vyplnily objem krychle. Jakou část objemu krychle vyplní? - Hranol 4b 2 Tělesová úhlopříčka pravidelného čtyřbokého hranolu svírá s podstavou úhel 60°. Hrana podstavy má délku 20 cm. Vypočtěte objem tělesa.
- Podstava
Podstavou kvádru je obdélník se stranou 7,5 cm a úhlopříčkou 12,5 cm. Objem kvádru je V = 0,9 dm³. Vypočtěte povrch kvádru. - Kosoštvorec podstava
Ypočítejte objem a povrch hranolu, jehož podstava je kosočtverec s úhlopříčkami u1 = 13 cm, u2 = 16 cm. Výška hranolu se rovná dvojnásobku podstavové hrany. - Podstavou
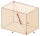Podstavou čtyřbokého hranolu je obdélník o rozměrech 3 dm a 4 dm. Výška hranolu je 1 m. Zjistěte jaký úhel svíra tělesová úhlopříčka s úhlopříčkou podstavy. - Kvádr - úhlopříčka
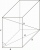Vypočítej objem kvádru, jehož tělesova úhlopříčka u se rovná 6,1cm a obdélníková postava má rozměry 3,2cm a 2,4cm - Hranol 23 Hranol ABCDA'B'C'D' má čtvercovou podstavu. Stěnová úhlopříčka AC podstavy má délku 9,9cm, tělesová úhlopříčka AC' má délku 11,4cm. Vypočítejte povrch a objem hranolu.
- Vzdálenost bodů
Je dán pravidelný čtyřboký jehlan ABCDV, ve kterém AB = a = 4 cm a v = 8 cm. Nechť S je střed CV. Vypočítejte vzdálenost bodů A a S. - Poloměr válce
Úhlopříčka osového řezu rotačního válce je 6 cm a jeho povrch je 30cm čtverečních. Vypočítej poloměr podstavy. - Poměr délky úhlopříček
Délky hran kvádru jsou v poměru 1:2:3. Budou ve stejném poměru i délky jeho stěnových úhlopříček? Kvádr má rozměry 5 cm, 10 cm a 15 cm. Vypočítejte velikost stěnových úhlopříček tohoto kvádru.
Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
