Úhel + Pythagorova věta - příklady a úlohy
Počet nalezených příkladů: 241
- Tři kamarádi 8
 Tři kamarádi sedí na molu, které je přesně uprostřed tekoucí řeky. prvni kamarád se vydává proti proudu řeky rychlostí 0,4 m/s, druhý kamarád se vydává po proudu řeky rychlostí 0,2 m/s, třetí kamarád pluje kolmo směrem ke břehu rychlostí 0,8 m/s. Rychlost
Tři kamarádi sedí na molu, které je přesně uprostřed tekoucí řeky. prvni kamarád se vydává proti proudu řeky rychlostí 0,4 m/s, druhý kamarád se vydává po proudu řeky rychlostí 0,2 m/s, třetí kamarád pluje kolmo směrem ke břehu rychlostí 0,8 m/s. Rychlost - V trojúhelníku 8
 V trojúhelníku ABC znáte poměr délek stran a:b:c=3:4:6. Vypočítejte velikosti úhlů trojúhelníku ABC.
V trojúhelníku ABC znáte poměr délek stran a:b:c=3:4:6. Vypočítejte velikosti úhlů trojúhelníku ABC. - Dvě silnice
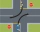 Dvě silnice spolu svírají pravý úhel. Na jedné silnici je 5km od křižovatky místo P, na druhé silnici je 12km od křižovatky místo R. Místa P a R jsou spojena přímou pěšinou. Chodec jde z místa R do místa P pěšinou průměrnou rychlostí 5km/h, auto jede z mí
Dvě silnice spolu svírají pravý úhel. Na jedné silnici je 5km od křižovatky místo P, na druhé silnici je 12km od křižovatky místo R. Místa P a R jsou spojena přímou pěšinou. Chodec jde z místa R do místa P pěšinou průměrnou rychlostí 5km/h, auto jede z mí - V rovině 2
 V rovině je umístěn trojúhelník ABC s pravým úhlem u vrcholu C, pro který platí: A(1, 2), B(5, 2), C(x, x+1), kde x > -1. a) určete hodnotu x b) určete souřadnice bodu M, který je středem úsečky AB c) dokažte že vektory AB a CM jsou kolmé d) určete vel
V rovině je umístěn trojúhelník ABC s pravým úhlem u vrcholu C, pro který platí: A(1, 2), B(5, 2), C(x, x+1), kde x > -1. a) určete hodnotu x b) určete souřadnice bodu M, který je středem úsečky AB c) dokažte že vektory AB a CM jsou kolmé d) určete vel
- Vypočítejte 248
 Vypočítejte objem a povrch pravidelného čtyřbokého hranolu o podstavné hraně a=24 cm, jestliže tělesová úhlopříčka svírá s podstavou úhel 66°
Vypočítejte objem a povrch pravidelného čtyřbokého hranolu o podstavné hraně a=24 cm, jestliže tělesová úhlopříčka svírá s podstavou úhel 66° - Trojuhelníku 135
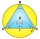 Trojuhelníku ABC o stranách a = 15 cm, b = 17,4 cm, c = 21,6 cm je opsána kružnice. Vypočítejte obsah úsečí určených stranami trojúhelníku.
Trojuhelníku ABC o stranách a = 15 cm, b = 17,4 cm, c = 21,6 cm je opsána kružnice. Vypočítejte obsah úsečí určených stranami trojúhelníku. - Tvar
 Určete goniometricky tvar komplexního čísla z = √ 23 -10 i
Určete goniometricky tvar komplexního čísla z = √ 23 -10 i - Vzdálenost 83160
 Vypočítej vzdálenost bodu A[ 4; 2; -3 ] od roviny : 2x - 2y + z + 5 = 0
Vypočítej vzdálenost bodu A[ 4; 2; -3 ] od roviny : 2x - 2y + z + 5 = 0 - Úhel mezi vektory
 Najděte úhel mezi danými vektory a zaokrouhlete výsledek na desetinu stupně. u = (-22, 11) a v = (16, 20)
Najděte úhel mezi danými vektory a zaokrouhlete výsledek na desetinu stupně. u = (-22, 11) a v = (16, 20)
- Cesta
 Na cestě je značka pro stoupání s úhlem 7%. Vypočtěte pod jakým úhlem (v stupních) cesta stoupá (klesá).
Na cestě je značka pro stoupání s úhlem 7%. Vypočtěte pod jakým úhlem (v stupních) cesta stoupá (klesá). - Trojúhelníku 50281
 Sestavte problém analytické geometrie, kde je třeba nalézt vrcholy trojúhelníku ABC: vrcholy tohoto trojúhelníku musí být body A (1,7) B (-5,1) C (5, -11). V uvedeném problému by se měly použít pojmy: vzdálenost od bodu k přímce, poměr dělení úsečky bodem
Sestavte problém analytické geometrie, kde je třeba nalézt vrcholy trojúhelníku ABC: vrcholy tohoto trojúhelníku musí být body A (1,7) B (-5,1) C (5, -11). V uvedeném problému by se měly použít pojmy: vzdálenost od bodu k přímce, poměr dělení úsečky bodem - Moivre 2
 Najděte třetí odmocniny z 125(cos 288° + i sin 288°).
Najděte třetí odmocniny z 125(cos 288° + i sin 288°). - Rovnostranný 3-uhelník
 Vypočítejte stranu rovnostranného trojúhelníku, jestliže jeho obsah je 1353 cm².
Vypočítejte stranu rovnostranného trojúhelníku, jestliže jeho obsah je 1353 cm². - Rovnostranný trojúhelník v2
 Rovnostranný trojúhelník má obvod 36 dm. Jaký má obsah?
Rovnostranný trojúhelník má obvod 36 dm. Jaký má obsah?
- Západ-jih
 Pozoroval stojící západně od věže vidí její vrchol pod výškovým úhlem 45 stupňů. Poté, co se posune o 50 metrů na jih, vidí její vrchol pod výškovým úhlem 30 stupňů. Jak vysoká je věž?
Pozoroval stojící západně od věže vidí její vrchol pod výškovým úhlem 45 stupňů. Poté, co se posune o 50 metrů na jih, vidí její vrchol pod výškovým úhlem 30 stupňů. Jak vysoká je věž? - Dvě těžnice
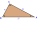 Pravoúhlý trojúhelník, úhel C je 90 stupňů. Znám těžnici ta = 8 cm a těžnici tb = 12 cm. .. Jak spočítat délku stran?
Pravoúhlý trojúhelník, úhel C je 90 stupňů. Znám těžnici ta = 8 cm a těžnici tb = 12 cm. .. Jak spočítat délku stran? - Lodník
 Po palubě lodí kráčí lodník stálou rychlostí 5 km/h ve směru, který svírá se směrem rychlosti lodi úhel 60°. Loď se pohybuje vzhledem ke klidné hladině jezera stálou rychlostí 10 km/h. Určete graficky velikost rychlosti, kterou se lodník pohybuje vzhledem
Po palubě lodí kráčí lodník stálou rychlostí 5 km/h ve směru, který svírá se směrem rychlosti lodi úhel 60°. Loď se pohybuje vzhledem ke klidné hladině jezera stálou rychlostí 10 km/h. Určete graficky velikost rychlosti, kterou se lodník pohybuje vzhledem - Vzdálenosti 6653
 Dvě přímé cesty se křižují a svírají úhel alfa = 53 stupňů 30'. Na jedné z nich stojí dva sloupy, jeden na křižovatce, druhý ve vzdálenosti 500m od ní. Jak daleko je třeba jít od křižovatky po druhé cestě, abychom viděli oba sloupy v zorném úhlu beta? a)
Dvě přímé cesty se křižují a svírají úhel alfa = 53 stupňů 30'. Na jedné z nich stojí dva sloupy, jeden na křižovatce, druhý ve vzdálenosti 500m od ní. Jak daleko je třeba jít od křižovatky po druhé cestě, abychom viděli oba sloupy v zorném úhlu beta? a) - Dvaja
 Dvě přímé čáry kříží v pravém úhlu. Dva lidé začínají současně v místě křižovatky. John jde rychlostí 4 km/h po jedné cestě a Peter jede rychlostí 8 km/h po druhé cestě. Jak dlouho bude trvat, než budou vzdálený 20√5 km od sebe?
Dvě přímé čáry kříží v pravém úhlu. Dva lidé začínají současně v místě křižovatky. John jde rychlostí 4 km/h po jedné cestě a Peter jede rychlostí 8 km/h po druhé cestě. Jak dlouho bude trvat, než budou vzdálený 20√5 km od sebe?
Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat.
