Searching in math word problems: ...
See also practice problems: angle, triangle, sine, The Law of Sines, right triangle, triangle inequality, similarity of triangles, The right triangle altitude theorem.We found these online calculators: sum of squares calculator (SST), average (mean) calculator, loan - mortgage.
Number of problems found: 0
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
For your searching, we found the following related math problems:
- Two triangles SSA
 We can form two triangles with the given information. Use the Law of Sines to solve the triangles. A = 59°, a = 13, b = 14
We can form two triangles with the given information. Use the Law of Sines to solve the triangles. A = 59°, a = 13, b = 14 - Area and two angles
 Calculate the size of all sides and internal angles of a triangle ABC if it is given by area S = 501.9; and two interior angles α = 15°28' and β = 45°.
Calculate the size of all sides and internal angles of a triangle ABC if it is given by area S = 501.9; and two interior angles α = 15°28' and β = 45°. - Mast shadow
 The mast has a 13 m long shadow on a slope rising from the mast foot in the direction of the shadow angle at an angle of 15°. Determine the height of the mast if the sun above the horizon is at an angle of 33°. Use the law of sines.
The mast has a 13 m long shadow on a slope rising from the mast foot in the direction of the shadow angle at an angle of 15°. Determine the height of the mast if the sun above the horizon is at an angle of 33°. Use the law of sines. - Inner angles
 The inner angles of the triangle are 30°, 45°, and 105° and its longest side is 10 cm. Calculate the shortest side length, and write the result in cm up to two decimal places.
The inner angles of the triangle are 30°, 45°, and 105° and its longest side is 10 cm. Calculate the shortest side length, and write the result in cm up to two decimal places. - Largest angle of the triangle
 Calculate the largest angle of the triangle whose sides have the sizes: 2a, 3/2a, 3a
Calculate the largest angle of the triangle whose sides have the sizes: 2a, 3/2a, 3a - Triangle's centroid
 In the triangle ABC the given lengths of its medians tc = 9, ta = 6. Let T be the intersection of the medians (triangle's centroid), and the point S is the center of the side BC. The magnitude of the CTS angle is 60°. Calculate the length of the BC side t
In the triangle ABC the given lengths of its medians tc = 9, ta = 6. Let T be the intersection of the medians (triangle's centroid), and the point S is the center of the side BC. The magnitude of the CTS angle is 60°. Calculate the length of the BC side t - Calculate triangle
 In the triangle, ABC, calculate the sizes of all heights, angles, perimeters, and area if given a=40cm, b=57cm, and c=59cm.
In the triangle, ABC, calculate the sizes of all heights, angles, perimeters, and area if given a=40cm, b=57cm, and c=59cm. - Cosine
 Cosine and sine theorem: Calculate all missing values from triangle ABC. c = 2.9 cm; β = 28°; γ = 14° α =? °; a =? cm; b =? cm
Cosine and sine theorem: Calculate all missing values from triangle ABC. c = 2.9 cm; β = 28°; γ = 14° α =? °; a =? cm; b =? cm - Cosine
 Cosine and sine theorem: Calculate all missing values (sides and angles) of the triangle ABC. a = 20 cm; b = 15 cm; γ = 90°; c =? cm; α =? °; β =? °
Cosine and sine theorem: Calculate all missing values (sides and angles) of the triangle ABC. a = 20 cm; b = 15 cm; γ = 90°; c =? cm; α =? °; β =? ° - Magnitudes 64704
 The triangle ABC determines the size of the sides a and b and the magnitudes of the interior angles β and γ, given c = 1.86 m, the line on the side c is 2.12 m, and the angle alpha is 40 ° 12 '.
The triangle ABC determines the size of the sides a and b and the magnitudes of the interior angles β and γ, given c = 1.86 m, the line on the side c is 2.12 m, and the angle alpha is 40 ° 12 '. - Inaccessible 69794
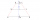 Determine the distance between two inaccessible places P, Q, if the distance between two observation points A, B is 2000m and if you know the size of the angles QAB = 52°40''; PBA = 42°01''; PAB = 86°40'' and QBA = 81°15''. The considered locations A, B,
Determine the distance between two inaccessible places P, Q, if the distance between two observation points A, B is 2000m and if you know the size of the angles QAB = 52°40''; PBA = 42°01''; PAB = 86°40'' and QBA = 81°15''. The considered locations A, B, - Triangle 75
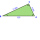 Triangle ABC has angle C bisected and intersected AB at D. Angle A measures 20 degrees, and angle B measures 40 degrees. The question is to determine AB-AC if length AD=1.
Triangle ABC has angle C bisected and intersected AB at D. Angle A measures 20 degrees, and angle B measures 40 degrees. The question is to determine AB-AC if length AD=1. - Solve 13
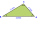 Solve the missing dimensions for the following triangle: Triangle ABC: AngleA=43 degrees, b=7.0cm, c=6.0cm Question 1. Angle B with units written as degrees Question 2. Angle C with units written as degrees Question 3. a, rounded to the nearest tenth of a
Solve the missing dimensions for the following triangle: Triangle ABC: AngleA=43 degrees, b=7.0cm, c=6.0cm Question 1. Angle B with units written as degrees Question 2. Angle C with units written as degrees Question 3. a, rounded to the nearest tenth of a - Rhomboid
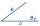 The rhomboid sides' dimensions are a= 5cm, b = 6 cm, and the angle's size at vertex A is 60°. What is the length of the side AC?
The rhomboid sides' dimensions are a= 5cm, b = 6 cm, and the angle's size at vertex A is 60°. What is the length of the side AC? - Calculate 4422
 Calculate the perimeter of the triangle ABC if a = 12 cm, the angle beta is 38 degrees, and the gamma is 92 degrees.
Calculate the perimeter of the triangle ABC if a = 12 cm, the angle beta is 38 degrees, and the gamma is 92 degrees. - Parallelogram 6049
 Calculate the area of the parallelogram if a = 57cm, the diagonal u = 66cm, and the angle against the diagonal is beta β = 57° 43'
Calculate the area of the parallelogram if a = 57cm, the diagonal u = 66cm, and the angle against the diagonal is beta β = 57° 43' - Triangle 35881
 The sum of the lengths of the two sides b + c = 12 cm Beta angle = 68 Gamma angle = 42 draw triangle ABC
The sum of the lengths of the two sides b + c = 12 cm Beta angle = 68 Gamma angle = 42 draw triangle ABC - Triangle's 9731
 Solve the triangle ABC if the side a = 52 cm, the height on the other side is vb = 21 cm, and the triangle's area is S = 330 cm².
Solve the triangle ABC if the side a = 52 cm, the height on the other side is vb = 21 cm, and the triangle's area is S = 330 cm². - The aspect ratio
 The aspect ratio of the rectangular triangle is 13:12:5. Calculate the internal angles of the triangle.
The aspect ratio of the rectangular triangle is 13:12:5. Calculate the internal angles of the triangle. - Determine 18223
 From the sine theorem, determine the ratio of the sides of a triangle whose angles are 30 °, 60 °, and 90 °.
From the sine theorem, determine the ratio of the sides of a triangle whose angles are 30 °, 60 °, and 90 °.
