Úsečky
Úsečky dĺžok 95 cm a 3,1 dm máme rozdeliť na rovnaké diely tak, aby ich dĺžka v centimetroch bola vyjadrená celým číslom. Koľkými spôsobmi ich môžeme deliť?
Správna odpoveď:
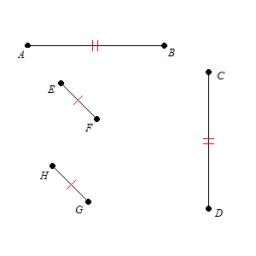
Tipy na súvisiace online kalkulačky
Chceš si vypočítať najväčší spoločný deliteľ dvoch alebo viacerých čísel?
Chcete premeniť jednotku dĺžky?
Chcete premeniť jednotku dĺžky?
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Ťažnica a výška
 Zostroj trojuholník KLM ak strana m=6,5cm, ťažnica tm=4cm, výška na stranu m: vm=3,2cm
Zostroj trojuholník KLM ak strana m=6,5cm, ťažnica tm=4cm, výška na stranu m: vm=3,2cm - ABCD(AB//CD): 70454
 Zostrojte lichobežník ABCD(AB//CD): |AB|=7cm |BC|=3,5cm |CD|=4cm A veľkosť uhla ABC=60°
Zostrojte lichobežník ABCD(AB//CD): |AB|=7cm |BC|=3,5cm |CD|=4cm A veľkosť uhla ABC=60° - Rozdeľte 6
 Rozdeľte úsečku AB na tri rovnaké časti. Návod: Zostrojte rovnostranný trojuholník ABC a nájdite jeho stred (napr. Opísanej kružnice).
Rozdeľte úsečku AB na tri rovnaké časti. Návod: Zostrojte rovnostranný trojuholník ABC a nájdite jeho stred (napr. Opísanej kružnice). - Bod na priamke
 Je daná priamka p a dva vnútorné body jednej z polrovín, určených priamkou p. Nájdi na priamke p bod X tak, aby súčet jeho vzdialeností od bodov A, B bol najmenší.
Je daná priamka p a dva vnútorné body jednej z polrovín, určených priamkou p. Nájdi na priamke p bod X tak, aby súčet jeho vzdialeností od bodov A, B bol najmenší.
- Narysuj 9
 Narysuj úsečku AB=14 cm a rozdeľte ju pomocou redukčného uhla v pomere 2:9.
Narysuj úsečku AB=14 cm a rozdeľte ju pomocou redukčného uhla v pomere 2:9. - Stred kružnice
 Je daná ľubovolná kružnica k, ktorá nemá vyznačený stred. Pomocou vhodnej konštrukcie nájdi stred kružnice k. Vyskúšaj na 2 rôznych kružniciach.
Je daná ľubovolná kružnica k, ktorá nemá vyznačený stred. Pomocou vhodnej konštrukcie nájdi stred kružnice k. Vyskúšaj na 2 rôznych kružniciach. - Narysuj 8
 Narysuj lichobežník, ak b=4cm, c=7cm, d=4,5cm, v= 3 cm (Postup, diskusia, náčrt, rozbor, konštrukcia)
Narysuj lichobežník, ak b=4cm, c=7cm, d=4,5cm, v= 3 cm (Postup, diskusia, náčrt, rozbor, konštrukcia) - Ukážte 2
 Ukážte (pomocou Menealovej vety), že ťažisko delí ťažnicu v pomere 1:2.
Ukážte (pomocou Menealovej vety), že ťažisko delí ťažnicu v pomere 1:2. - ZIMA
 Mám pravouhlý lichobežník ZIMA (pravý uhol pri vrchole Z) ZI-7cm, ZM-5cm, AM-3,5cm a mám napísať aj postup a spraviť skúšku v konštrukčnej úlohe
Mám pravouhlý lichobežník ZIMA (pravý uhol pri vrchole Z) ZI-7cm, ZM-5cm, AM-3,5cm a mám napísať aj postup a spraviť skúšku v konštrukčnej úlohe
- C-I-2 2018 MO
 Na strane AB trojuholníka ABC sú dané body D a E tak, že |AD| = |DE| = |EB|. Body A a B sú postupne stredmi úsečiek CF a CG. Priamka CD pretína priamku FB v bode I a priamka CE pretína priamku AG v bode J. Dokážte, že priesečník priamok AI a BJ leží na pr
Na strane AB trojuholníka ABC sú dané body D a E tak, že |AD| = |DE| = |EB|. Body A a B sú postupne stredmi úsečiek CF a CG. Priamka CD pretína priamku FB v bode I a priamka CE pretína priamku AG v bode J. Dokážte, že priesečník priamok AI a BJ leží na pr - Kosodĺžnik 8
 Zostroj rovnobežník (kosodĺžnik) ABCD, |AB|= 4 cm alfa=30° |BD|= 5 cm.
Zostroj rovnobežník (kosodĺžnik) ABCD, |AB|= 4 cm alfa=30° |BD|= 5 cm. - Rovnakých 6890
 Úsečka MN (/MN/ = 9cm) rozdeľte na 11 rovnakých dielikov
Úsečka MN (/MN/ = 9cm) rozdeľte na 11 rovnakých dielikov - Narysuj 4
 Narýsuj úsečku KL=55mm. Narýsuj kružnicu k so stredom K a polomerom 4cm. Vyznačuj body tak, aby patrili kružnici a spájaj ich s bodom L.
Narýsuj úsečku KL=55mm. Narýsuj kružnicu k so stredom K a polomerom 4cm. Vyznačuj body tak, aby patrili kružnici a spájaj ich s bodom L. - Rovnoramenný lichobežník 9
 Narysuj rovnoramenný lichobežník ABDC, ak a=6cm, v=5cm, beta=60 stupňov. /náčrt, postup, konštrukcia/
Narysuj rovnoramenný lichobežník ABDC, ak a=6cm, v=5cm, beta=60 stupňov. /náčrt, postup, konštrukcia/
- Dorysuj 5456
 Dorysuj úsečku AB, ak poznáš jeden jej krajný bod a stred úsečky S.
Dorysuj úsečku AB, ak poznáš jeden jej krajný bod a stred úsečky S. - Kosoštvorec
 Skonštruujte kosoštvorec EFGH, kde e = 6,7cm, výška na stranu h: v = fh = 5cm
Skonštruujte kosoštvorec EFGH, kde e = 6,7cm, výška na stranu h: v = fh = 5cm - Kružnice 7
 Zostroj kružnice k1 (S1;r1) a k2(S2;r2), ak S1 S2 = 7 cm, d1= 12cm a r2 = 1/2 r1. Vyznač bod : a) A ležiaci na kružnici k1, b) B ležiaci v oboch kruhoch určených kružnicami k1 a k2, c) C ležiaci súčasne na oboch kružniciach, d) D, pre ktorý platí: (S1D)=
Zostroj kružnice k1 (S1;r1) a k2(S2;r2), ak S1 S2 = 7 cm, d1= 12cm a r2 = 1/2 r1. Vyznač bod : a) A ležiaci na kružnici k1, b) B ležiaci v oboch kruhoch určených kružnicami k1 a k2, c) C ležiaci súčasne na oboch kružniciach, d) D, pre ktorý platí: (S1D)=
