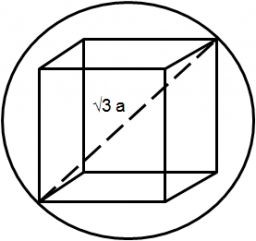
Kocka 59
Kocka má povrch 600 cm2, aký je jej objem?
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Tip: premeniť jednotky objemu vám pomôže naša kalkulačka premeny jednotiek objemu.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Kocka
Súčet dĺžok hrán kocky je 30 cm. Aký je jej povrch a objem? - Spotrebovaných 82606
Papierová krabica má tvar kocky. Na jej výrobu bolo spotrebovaných 2400 cm². Ohyby na prilepenie stien sa nezapočítavajú. Aký je objem krabice? - Otvorená
Otvorená krabička má tvar kocky. Na jej oblepenie spotrebovali 80 dm² papiera. Aký je objem tejto krabičky? - Pretvorených 5992
Päťdesiat malých kovových kocôčok s dĺžkou hrany 2cm bolo pretvorených az tejto hmoty bola vyrobená jedna veľká kocka. Aký je jej povrch?
Kocka má povrch 5400 cm² . Aká je dížka jej hrany a objem kocky?
Hrana kocky, ktorej objem je 58,3% jej povrchu je : a)3,5cm b) 4,5cm č) 2,5cm d) 1,5cm
Kocka má povrch 384 cm². Vypočítaj jej objem.