Rovnica
Koľko reálnych koreňov má rovnica x3=x?
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Rovnica s absolútnou hodnotou
 Koľko riešení má rovnica (|x| +x) |x-3| = |x+1| v obore reálnych čísel?
Koľko riešení má rovnica (|x| +x) |x-3| = |x+1| v obore reálnych čísel? - Rovnica
 Rovnica f(x) = 0 má korene x1 = 64, x2 = 100, x3 = 25, x4 = 49. Koľko je všetkých koreňov rovnice f(x²) = 0 ?
Rovnica f(x) = 0 má korene x1 = 64, x2 = 100, x3 = 25, x4 = 49. Koľko je všetkých koreňov rovnice f(x²) = 0 ? - Súčin a súčet koreňov
 Nájdite súčin a súčet koreňov kvadratickej rovnice x² + 3x - 9 = 0 Aplikujte vzťahy medzi koreňmi a koeficientami kvadratickej rovnice.
Nájdite súčin a súčet koreňov kvadratickej rovnice x² + 3x - 9 = 0 Aplikujte vzťahy medzi koreňmi a koeficientami kvadratickej rovnice. - Koreň 6
 Určte menší koreň z dvojice koreňov sústavy rovníc. 5a + 4b =11 3a - 2b = 11
Určte menší koreň z dvojice koreňov sústavy rovníc. 5a + 4b =11 3a - 2b = 11
- Exponenciálna rovnica
 Riešte exponenciálnu rovnicu (v obore reálnych čísel): 98x-2=9
Riešte exponenciálnu rovnicu (v obore reálnych čísel): 98x-2=9 - Počet koreňov
 Dosaď postupne čísla/0,1,2,3/do rovnice: (X - 1) (x - 3) (x + 1) = 0 Ktorá z nich sú jej riešením? Existuje ešte ďalšie číslo, ktoré je riešením tejto rovnice?
Dosaď postupne čísla/0,1,2,3/do rovnice: (X - 1) (x - 3) (x + 1) = 0 Ktorá z nich sú jej riešením? Existuje ešte ďalšie číslo, ktoré je riešením tejto rovnice? - Floor zaokrúhľovanie nadol
 V obore reálnych čísel riešte sústavu rovníc: 2x + ⌊y⌋ = 2022, 3y + ⌊2x⌋ = 2023. (⌊a⌋ označuje (dolnú) celú časť reálneho čísla a, t. j. najväčšie celé číslo, ktoré nie je väčšie ako a. Napr. ⌊1,9⌋ = 1 a ⌊−1,1⌋ = −2.)
V obore reálnych čísel riešte sústavu rovníc: 2x + ⌊y⌋ = 2022, 3y + ⌊2x⌋ = 2023. (⌊a⌋ označuje (dolnú) celú časť reálneho čísla a, t. j. najväčšie celé číslo, ktoré nie je väčšie ako a. Napr. ⌊1,9⌋ = 1 a ⌊−1,1⌋ = −2.) - Tretiu s druhou
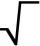 Máme 2 čísla. Keby sme vynásobili tretiu odmocninu prvého čísla s druhou odmocninou druhého čísla, dostali by sme číslo 18.Určte tieto 2 čísla. Ak má úloha v množine reálnych čísel nekonečne veľa riešení, vypočítajte len celočíselné riešenie.
Máme 2 čísla. Keby sme vynásobili tretiu odmocninu prvého čísla s druhou odmocninou druhého čísla, dostali by sme číslo 18.Určte tieto 2 čísla. Ak má úloha v množine reálnych čísel nekonečne veľa riešení, vypočítajte len celočíselné riešenie. - Odmocninka
 Peter mal v mysli číslo a povedal:Keď toto neznáme číslo vydelím treťou odmocninou čísla 27 a následne vynásobim tromi, dostanem neznáme číslo. Aké číslo si Peter myslel?
Peter mal v mysli číslo a povedal:Keď toto neznáme číslo vydelím treťou odmocninou čísla 27 a následne vynásobim tromi, dostanem neznáme číslo. Aké číslo si Peter myslel?
- Postupnosť 80450
 Koľko členov má postupnosť, ak je dané a1=4, Sn=589, d=3, n=?
Koľko členov má postupnosť, ak je dané a1=4, Sn=589, d=3, n=? - Podiel 12
 Podiel trojnásobku čísla x a dvojnásobku čísla 9 sa rovná 3. Akú hodnotu má číslo x?
Podiel trojnásobku čísla x a dvojnásobku čísla 9 sa rovná 3. Akú hodnotu má číslo x? - Peťko 2
 Peťko má trikrát viac cukríkov ako jeho kamarát Maťko. Keď obom zobral Peťkov brat Ferko po 4 cukríky, mal ich Peťko päťkrát viac ako Maťko. Koľko cukríkov má Peťko teraz?
Peťko má trikrát viac cukríkov ako jeho kamarát Maťko. Keď obom zobral Peťkov brat Ferko po 4 cukríky, mal ich Peťko päťkrát viac ako Maťko. Koľko cukríkov má Peťko teraz? - Priesečníky 25141
 Kvadratická funkcia má predpis y=x²-2x-3. Načrtnite graf tejto funkcie. Určite priesečníky s osami. Určite súradnice vrcholu.
Kvadratická funkcia má predpis y=x²-2x-3. Načrtnite graf tejto funkcie. Určite priesečníky s osami. Určite súradnice vrcholu. - Euklid1
 Pravouhlý trojuholník má preponu c = 27 cm. Ako veľké úseky vytína výška vc = 3 cm na prepone c?
Pravouhlý trojuholník má preponu c = 27 cm. Ako veľké úseky vytína výška vc = 3 cm na prepone c?
- Oco a ivo
 Riešte rovnicu: oco + ivo = cita Koľko má úloha riešení?
Riešte rovnicu: oco + ivo = cita Koľko má úloha riešení? - Lichobežník 5341
 Lichobežník, kde AB je rovnobežná s CD, má uhol A : uhol D = 4 : 5, uhol B = 3x-15 a uhol C = 4x+20. Nájdite uhol A, B, C a D.
Lichobežník, kde AB je rovnobežná s CD, má uhol A : uhol D = 4 : 5, uhol B = 3x-15 a uhol C = 4x+20. Nájdite uhol A, B, C a D. - Počet riešení
 Koľko riešení má rovnica x . y = 2950 s dvoma neznámymi v množine prirodzených čísel
Koľko riešení má rovnica x . y = 2950 s dvoma neznámymi v množine prirodzených čísel
