Tetiva
Určite polomer kružnice v ktorej tetiva vzdialená 8 cm od stredu kružnice je o 11 cm dlhšia ako polomer kružnice.
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Hľadáte pomoc s výpočtom koreňov kvadratickej rovnice?
Pytagorova veta je základ výpočtov aj kalkulačky pravouhlého trojuholníka.
Pytagorova veta je základ výpočtov aj kalkulačky pravouhlého trojuholníka.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Tetiva MN
 Tetiva MN kružnice je od stredu kružnice S vzdialená 182 cm. Uhol MSN má veľkosť 30°. Určite polomer kružnice.
Tetiva MN kružnice je od stredu kružnice S vzdialená 182 cm. Uhol MSN má veľkosť 30°. Určite polomer kružnice. - Tetiva 5
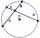 Vypočítaj dĺžku tetivy kružnice, ktorá je vzdialená od stredu kružnice 2,5 cm. Polomer je 6,5 cm.
Vypočítaj dĺžku tetivy kružnice, ktorá je vzdialená od stredu kružnice 2,5 cm. Polomer je 6,5 cm. - Dve tetivy
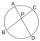 V kružnici sú vedené dve tetivy dlhé 30 a 34 cm. Kratšia z nich je od stredu dvakrát ďalej než dlhšia. Urči polomer kružnice.
V kružnici sú vedené dve tetivy dlhé 30 a 34 cm. Kratšia z nich je od stredu dvakrát ďalej než dlhšia. Urči polomer kružnice. - Tetiva 5
 Je daná kružnica k / S; 5 cm /. Jej tetiva MN je vzdialená od stredu kružnice 3 cm. Vypočítajte jej dĺžku.
Je daná kružnica k / S; 5 cm /. Jej tetiva MN je vzdialená od stredu kružnice 3 cm. Vypočítajte jej dĺžku.
- Vypočítajte 4228
 Je daná kružnica k (S, 5cm). Vypočítajte dĺžku tetivy kružnice k, ak je od stredu S vzdialená 3cm.
Je daná kružnica k (S, 5cm). Vypočítajte dĺžku tetivy kružnice k, ak je od stredu S vzdialená 3cm. - Tetiva 3
 Aký polomer má kružnica, ak jej tetiva je vzdialená od stredu o 2/3 polomeru a má dĺžku 10cm?
Aký polomer má kružnica, ak jej tetiva je vzdialená od stredu o 2/3 polomeru a má dĺžku 10cm? - Tetiva 6
 Tetiva dlhá 16 cm je od stredu kružnice vzdialená 6 cm. Vypočítajte dĺžku kruznice.
Tetiva dlhá 16 cm je od stredu kružnice vzdialená 6 cm. Vypočítajte dĺžku kruznice. - Tetiva
 Vypočítaj dĺžku tetivy, ktorej vzdialenosť od stredu S kružnice k (S, 8 cm) sa rovná 7 cm.
Vypočítaj dĺžku tetivy, ktorej vzdialenosť od stredu S kružnice k (S, 8 cm) sa rovná 7 cm. - Vzdialenosť 79144
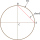 Polomer kružnice r=8,9 cm, tetiva AB tejto kružnice má dĺžku 16 cm. Vypočítaj vzdialenosť tetivy AB od stredu kružnice.
Polomer kružnice r=8,9 cm, tetiva AB tejto kružnice má dĺžku 16 cm. Vypočítaj vzdialenosť tetivy AB od stredu kružnice.
- Tetiva
 Akú dĺžku má tetiva AB, ktorej vzdialenosť od stredu S kružnice k(S, 92 cm) sa rovná 10 cm?
Akú dĺžku má tetiva AB, ktorej vzdialenosť od stredu S kružnice k(S, 92 cm) sa rovná 10 cm? - Tetiva
 Akú dĺžku x má tetiva kružnice s priemerom 60 m, ak je vzdialená od stredu kružnice 10 m?
Akú dĺžku x má tetiva kružnice s priemerom 60 m, ak je vzdialená od stredu kružnice 10 m? - Tetiva 5
 Vypočítajte dĺžku tetivy kružnice s polomerom r = 10 cm, ktorej dĺžka sa rovná jej vzdialenosti od stredu kružnice.
Vypočítajte dĺžku tetivy kružnice s polomerom r = 10 cm, ktorej dĺžka sa rovná jej vzdialenosti od stredu kružnice. - Tetiva
 V kružnici s polomerom 10 cm je 12 cm dlhá tetiva. Vypočítaj vzdialenosť tetivy od stredu kružnice.
V kružnici s polomerom 10 cm je 12 cm dlhá tetiva. Vypočítaj vzdialenosť tetivy od stredu kružnice. - Tetivka
 Vypočítaj vzdialenosť tetivy dlhej 19 cm od stredu kružnice s priemerom 28 cm.
Vypočítaj vzdialenosť tetivy dlhej 19 cm od stredu kružnice s priemerom 28 cm.
- Tetiva
 V kružnici k (S; 6cm) vypočítajte vzdialenosť tetivy t od stredu kružnice S, ak dĺžka tetivy je t= 10cm.
V kružnici k (S; 6cm) vypočítajte vzdialenosť tetivy t od stredu kružnice S, ak dĺžka tetivy je t= 10cm. - Tetiva 16
 Je daná kružnica k (S, r=6cm) a na nej bodmi A, B tak, že /AB/ = 8cm. Vypočítaj vzdialenosť stredu S kružnice k od stredu C úsečky AB.
Je daná kružnica k (S, r=6cm) a na nej bodmi A, B tak, že /AB/ = 8cm. Vypočítaj vzdialenosť stredu S kružnice k od stredu C úsečky AB. - Dve rovnobežné
 Dve rovnobežné tetivy kružnice majú rovnakú dĺžku 6 cm a sú od seba vzdialené 8 cm. Vypočítaj polomer kružnice.
Dve rovnobežné tetivy kružnice majú rovnakú dĺžku 6 cm a sú od seba vzdialené 8 cm. Vypočítaj polomer kružnice.
