Uhlopriečka + pravouhlý trojuholník - príklady a úlohy - strana 11 z 18
Počet nájdených príkladov: 346
- Po búrke
Pána Radomíra pri poslednej búrke postihlo nešťastie, na strechu tvaru pravidelného štvorbokého ihlanu mu spadol strom a celú mu ju zničil. Strecha má podstavou dĺžku hrany 8m a dĺžku bočnej hrany 15m. Koľko m² strešnej krytiny bude musieť nakúpiť? - Guľa a kúžel
Do gule s polomerom G = 41 cm vpíšte kužel s najväčším objemom. Aký je tento objem a aké sú rozmery kužela? - Pravidelný 6B hexagón
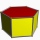Drôtený model pravidelného šesťbokového hranola s podstavnou hranou dĺžky a = 8 cm má výšku v = 12 cm. Teleso sa prelepí papierom, podstavy tmavým a plášť bielym. - Vypočítajte v cm najväčšiu možnú priamu vzdialenosť dvoch vrcholov drôteného hranola (hrúb - Kov modelu
Peter si z dovolenky v Egypte priviezol model pyramídy v tvare pravidelného štvorbokého ihlanu. Zmeral si že jej podstavná hrana má dĺžku 7cm a bočné hrany majú dĺžku 10 cm. Model má hmotnosť 1kg a je vyrobený z neznámeho kovu. Z akého kovu je model vyrob - Kvetinový záhon
Kvetinový záhon má tvar zrezaného ihlana, pričom hrana dolnej podstavy a= 10 m, hornej podstavy b= 9 m a odchýlka počnej hrany od podstavy je alfa= 45°. Aký objem zemniny je potrebný navýšiť na tento záhon? Koľko sadeníc je možné vysadiť, ak 1m²= 100 sade - Stĺp
Vypočítajte objem a povrch podporného stĺpu tvare kolmého štvorbokého hranola, ktorého podstavou je kosoštvorec s uhlopriečku u1 = 102cm, u2 = 64cm. Výška stĺpa je 1,5m. - Štvorboký ihlan - objem a povrch
V pravidelnom štvorbokom ihlane je výška 6,5 cm a uhol medzi podstavou a bočnou stenou je 42°. Vypočítaj povrch a objem telesa. Výpočty zaokrúhliť na 1 desatinné miesto. - Kosý hranol
Aký objem má štvorboký kosý hranol s podstavnými hranami o dĺžke a = 1m, b = 1,1m, c = 1,2 m, d = 0,7m, ak bočná hrana s dĺžkou h = 3,9 m má odchýlku od podstavy 20°35' a hrany a, b zvierajú uhol 50,5°? - Sily
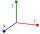Na bod I pôsobia tri navzájom kolmé sily F1=6 N, F2=15 N, F3=20 N. Určte výslednicu F a uhly, ktoré zviera výslednica so zložkami F1, F2, F3. - Matematika 2
Do prepravného kontajnera s rozmermi a=10 m, b=4m, c=3m bola umiestnená drevená debna s rozmermi d=3m, e=4m a f=3m. Aká je maximálna dĺžka rovnej neohybnej tyče so zanedbateľným priemerom, ktorú je možné v tejto situácii ešte do kontejnera umiestniť? - Kváder
Vypočítajte objem a povrch kvádra ABCDEFGH, ktorého rozmery abc sú v pomere 9:4:8, ak viete že stenová uhlopriečka AC meria 95 cm a má od telesovej uhlopriečky AG má odchýlku 30 stupňov. - Zrezaný ihlan
Vypočítaj povrch a objem pravidelného štvorbokého zrezaného ihlanu: a1 = 18 cm, a2 = 6cm / uhol alfa / α = 60 ° (Uhol α je uhol medzi bočnou stenou a rovinou podstavy.) S =? , V =? - Rozdiel objemov
Do valca s výškou 10 centimetrov je vložený kváder so štvorcovou podstavou tak že jeho podstavava je vpísaná do podstavy valca. Hrana podstavy kvádra meria 4 cm. Obe telesá majú rovnakú výšku. Vypočítajte rozdiel objemov valca a kvádra - Podstava kosoštvorec
Vypočítajte objem a povrch hranola, ktorého podstava je kosoštvorec s uhlopriečkami u1 = 12 cm, u2 = 14 cm. Výška hranola sa rovná dvojnásobku podstavovej hrany. - Výška 18
Výška pravidelného štvorbokého hranola je v=10 cm, odchýlka telesovej uhlopriečky od podstavy je 60°. Určte dĺžku podstavových hrán, povrch a objem kvádra. - Guľatina
Priemer kmeňa je 85 cm. Je možné z neho vytesať hranol s podstavou štvorca o strane 62 cm? - Pravidelný 4BH
Pravidelný štvorboký hranol má objem 864 cm³ a obsah jeho plášťa je dvojnásobkom obsahu jeho podstavy. Určte veľkosť jeho telesovej uhlopriečky. - Štvorboký ihlan v2
Vypočítajte objem a povrch pravidelného štvorbokého ihlanu ak je obsah podstavy 20 cm² a odchýlka bočnej hrany od roviny podstavy je 60 stupňov. - Borovica - drevo
Z kmeňa borovice dlhej 6 m s priemerom 35 cm sa má vyrezať trám s priečnym rezom v tvare štvorca tak, aby štvorec mal čo najväčší obsah. Vypočítajte dĺžku strany štvorca. Vypočítajte objem trámu v metroch kubických. - Debna
Debnu tvaru hranola s výškou 1 m a štvorcovou podstavou s hranou 0,6 m preklopíme účinkom sily 350 N, ktorá pôsobí vodorovne oproti hornej hrane. Akú hmotnosť má debna?
Máš príklad, ktorý si tu nenašiel vyriešenú? Pošli nám tento príklad a my Ti ho skúsime vypočítať.
