Rozdiel objemov
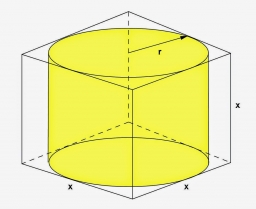
Do valca s výškou 10 centimetrov je vložený kváder so štvorcovou podstavou tak že jeho podstavava je vpísaná do podstavy valca. Hrana podstavy kvádra meria 4 cm. Obe telesá majú rovnakú výšku. Vypočítajte rozdiel objemov valca a kvádra
Vaša odpoveď:
Vaša odpoveď:
Tipy na súvisiace online kalkulačky
Tip: premeniť jednotky objemu vám pomôže naša kalkulačka premeny jednotiek objemu.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
aritmetikastereometriaplanimetriaJednotky fyzikálnych veličínÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Odvŕtané z kvádra
Do kvádra s výškou 50 cm so štvorcovou podstavou o hrane dĺžky 20 cm je vyvŕtaný otvor tvaru valca s priemerom 12 cm. Os tohto otvoru prechádza stredmi podstav kvádra. Vypočítajte objem a povrch takto vzniknutého telesa. - Máme kváder
Máme kváder so štvorcovou podstavou a výškou 12 dm. Vieme, že jeho objem je 588 dm kubických. Vypočítajte povrch kvádra s rovnakou podstavou, ale o 2 cm väčšou výškou. Výsledok napíšete v dm². - Ihlan
Aký je povrch pravidelného ihlana so štvorcovou podstavou, ak každá hrana podstavy meria 40 mm, výška sklonu ihlana je 44 mm a výška ihlana je 38 mm? - Kváder 50
Kváder so štvorcovou podstavou dĺžkou hrany 4 dm má povrch 112 dm štvorcových. Urč jeho výšku. - Akvárium
Doma máme akvárium tvaru kvádra so štvorcovou podstavou a otec nalial doň 70 litrov vody. Dĺžka hrany podstavy je 36 cm. Do akej výšky siaha voda? - Vzdialenosť hladiny
Nádrž na vodu má tvar kvádra so štvorcovou podstavou (hrana podstavy má dĺžku 3,2 m). Výška nádrže je 3 m. Aká je vzdialenosť hladiny vody od hornej podstavy, ak je v nádrži 25 600 litrov vody? - Mimozemská loď
Mimozemská loď má tvar gule o polomere r = 3000 m a jej posádka potrebuje loďou odviezť nazbieraný výskumný materiál v boxe v tvare kvádra so štvorcovou podstavou. Určte dĺžku podstavy a (a výšku h) tak, aby mal box najväčší možný objem.
