Jehlan 8
Vypočítej objem a povrch pravidelného čtyřbokého jehlanu se stranou podstavy 9 cm, boční stěna svírá s podstavou úhel 75°.
Vaše odpověď:
Vaše odpověď:
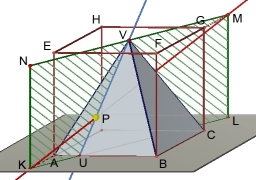
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebrastereometrieplanimetriegoniometrie a trigonometrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Boční stěna - jehlan
Vypočítejte objem jehlanu, jehož hrana podstavy a = 8 cm a boční stěna svírá se čtvercovou podstavou úhel α = 60°. - Komolý jehlan
Vypočítejte objem pravidelného 4-bokeho komolého jehlanu, jestliže a1 = 14 cm, a2 = 8 cm a úhel, který svírá boční stěna s podstavou je 42 stupňů. - Střecha
Střecha věže má tvar pravidelného čtyřbokého jehlanu, jehož podstavná hrana je dlouhá 11 m a boční stěna svírá s podstavou úhel velikosti 57°. Vypočtěte kolik krytiny potřebujeme na pokrytí celé střechy, pokud počítáme s 15% -ním odpadem. - Jehlan 6
Vypočítej povrch a objem pravidelného čtyřbokého komolého jehlanu : a1= 18 cm , a2=6 cm /úhel alfa/α=60° (Úhel α je úhel mezi boční stěnou a rovinou podstavy.) S=? , V=? - Tělesová
Tělesová úhlopříčka pravidelného čtyřbokého hranolu svírá s podstavou úhel velikosti 60°. Hrana podstavy má délku 10 cm. Vypočítejte objem tělesa. - Vypočítej 391
Vypočítej objem pravidelného čtyřbokého jehlanu s podstavou čtverce o straně a = 3 cm a délkou boční hrany b = 7 cm - Hranol 4b 2
Tělesová úhlopříčka pravidelného čtyřbokého hranolu svírá s podstavou úhel 60°. Hrana podstavy má délku 20 cm. Vypočtěte objem tělesa.
