Aritmeticka i geometrická
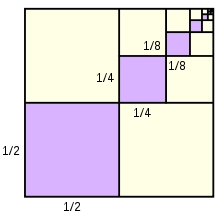
Tři čísla, které tvoří aritmetickou posloupnost, mají součet 30. Pokud odečteme od prvního 5, od druhého 4 a třetí ponecháme, dostaneme geometrickou posloupnost. Urči členy AP i GP.
Vaše odpověď:
Vaše odpověď:
Tipy na související online kalkulačky
Hledáte pomoc s výpočtem aritmetického průměru?
Hledáte statistickou kalkulačku?
Hledáte pomoc s výpočtem kořenů kvadratické rovnice?
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Hledáte statistickou kalkulačku?
Hledáte pomoc s výpočtem kořenů kvadratické rovnice?
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Geometrická posloupnost
Členy 1/64, 1/32, 1/16 tvoří geometrickou posloupnost (GP) Pokud je součet GP (2³6 – 2-6), najděte počet členů. - Geometrická posloupnost
Odečteme-li od čísel 33, 45 a 63 totéž číslo, dostaneme tři za sebou jdoucí členy GP. Určete tuto GP a vypočítejte její pátý člen. - Aritmetická posloupnost tyčí
Délky dvanácti pólů tvoří aritmetickou posloupnost (AP). Pokud je třetí pól 3 m a osmý pól 5 m, najděte: (i) Délka první tyče (ii) Součet délek tyčí - Čtyři čísla se součtem a vlastnostmi
Najděte taková čtyři čísla, jejichž součet je 48 a která mají tyto vlastnosti: když od prvního odečteme 3, k druhému přičteme 3, třetí vynásobíme třemi a čtvrté vydělíme třemi, dostaneme stejný výsledek. - Aritmetická posloupnost Tři čísla, která tvoří tři za sebou následující členy aritmetické posloupnosti mají součet 60 a součin 7500. Urči tato čísla.
- Je dána
Je dána posloupnost, jejíž první tři členy jsou a1= 70, a2=64, a3=58. 1, rozhodnete, zda se jedna o aritmetickou či geometrickou posloupnost a podle toho určete hodnotu d respektive q. 2, určete hodnotu patnáctého členů posloupnosti. 3, určete, kolikátý č - Čtyřúhelník - AP úhly
Čtyři úhly čtyřúhelníku tvoří aritmetickou posloupnost. Pokud je společný rozdíl 15°, najděte všechny jeho úhly.
