Draky
Kluci si pouštěli draka na šňůře 27 metrů dlouhé. Jako vysoce poletuje drak, když úhel od vodorovné roviny je 51°?
Správná odpověď:
Tipy na související online kalkulačky
Chcete proměnit jednotku délky?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
planimetriegoniometrie a trigonometrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Související a podobné příklady:
- Drak
Děti mají draka na šňůře dlouhé 80m, který se vznáší nad místem vzdáleným 25m od místa kde stojí děti. Jak vysoko se vznáší drak nad terénem? - Pozorovatel 11
Pozorovatel vidí letadlo pod výškovým úhlem 35° (úhel od vodorovné roviny). V tu chvíli letadlo hlásí výšku 4 km. Jak daleko od pozorovatele je místo, nad kterým letadlo letí. Zaokrouhli na stovky metrů. - Úhly deltoidu z draka
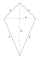Papírový drak má tvar deltoidu ABCD, ve kterém jsou dvě kratší strany dlouhé po 30 cm, dvě delší strany po 51 cm a kratší úhlopříčka má délku 48 cm. Určete velikosti vnitřních úhlů daného deltoidu. - Délka běhu na tréninku
Kolik metrů proběhli kluci, když na fotbalovém tréninku třikrát oběhli hřiště, které je 100 m dlouhé a 60 m široké? - Délka stínu
Vypočítejte délku stínu, který vrhá metrová tyč v pravé poledne, nacházející se na rovině poledníku a odchýlená od vodorovné roviny k severu o úhel velikosti 70°, pokud Slunce kulminuje pod úhlem 41°03'. - Rádiova anténa
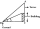Avanti se snaží nalézt výšku rádiové antény na střeše místní budovy. Stojí ve vodorovné vzdálenosti 21 metrů od budovy. Úhel elevace od jejího očí ke střeše (bod A) je 42° a úhel elevace od jejího očí k vrcholu antény (bod B) je 51°. Pokud jsou její oči 1 - Drak
Janko má draka, který je tvaru kosočtverce. Jeho úhlopříčky jsou dlouhé 60 cm a 90 cm. Vypočítejte: a) stranu kosočtverce b) kolik papíru potřebuje Janko na draka, pokud jej potřebuje oblepit z obou stran a na zahnutí potřebuje 5% z celkové plochy papíru.
