Pythagorova věta - slovní úlohy a příklady - strana 50 z 73
Počet nalezených příkladů: 1444
- Střecha
 Střecha kostelní věže má tvar pravidelného čtyřbokého jehlanu s podstavnou hranou délky 5,4m a výškou 5m. Bylo zjištěno, že bude třeba opravit 27% krytiny na střešní ploše. Jaké množství materiálu bude třeba?
Střecha kostelní věže má tvar pravidelného čtyřbokého jehlanu s podstavnou hranou délky 5,4m a výškou 5m. Bylo zjištěno, že bude třeba opravit 27% krytiny na střešní ploše. Jaké množství materiálu bude třeba? - Kulový odsek a výsek
 Vypočtěte povrch kulového výseku, pokud kulový odsek, který je částí výseku, má poloměr podstavy ρ = 9 cm a výšku v = 2,4 cm.
Vypočtěte povrch kulového výseku, pokud kulový odsek, který je částí výseku, má poloměr podstavy ρ = 9 cm a výšku v = 2,4 cm. - Štvobokého 83259
 Obvod štvobokého ihlava je 48 m a jeho výška je 2,5 m; kolik bude stát plech na tento jehlan, když 1 m² stojí 1,5 €; do plochy se počítá i 12% ztráta na spoje a záhyby.
Obvod štvobokého ihlava je 48 m a jeho výška je 2,5 m; kolik bude stát plech na tento jehlan, když 1 m² stojí 1,5 €; do plochy se počítá i 12% ztráta na spoje a záhyby. - Pravidelného 71484
 Střecha věže má tvar pravidelného 4-bokého jehlanu a výškou 4m a hranou podstavy 6m. Zjistilo se, že je poškozeno 25% krytiny na střeše. Kolik metrů čtverečních krytiny je potřeba k opravě střechy?
Střecha věže má tvar pravidelného 4-bokého jehlanu a výškou 4m a hranou podstavy 6m. Zjistilo se, že je poškozeno 25% krytiny na střeše. Kolik metrů čtverečních krytiny je potřeba k opravě střechy? - Spotrebovalo 7910
 Střecha rekreační chaty má tvar pravidelného čtyřbokého jehlanu o výšce 8m a podstavnou hranou 4m. Kolik ℅ připadlo na záhyby a spoje pokud se na pokrytí střechy spotřebovalo 75,9 metrů čtverečních plechu?
Střecha rekreační chaty má tvar pravidelného čtyřbokého jehlanu o výšce 8m a podstavnou hranou 4m. Kolik ℅ připadlo na záhyby a spoje pokud se na pokrytí střechy spotřebovalo 75,9 metrů čtverečních plechu? - Střecha
 2/3 plochy střechy ve tvaru pravidelného čtyřbokého jehlanu s hranou podstavy 9 m a výškou 6 m je už pokryta krytinou. Kolik třeba ještě pokrýt?
2/3 plochy střechy ve tvaru pravidelného čtyřbokého jehlanu s hranou podstavy 9 m a výškou 6 m je už pokryta krytinou. Kolik třeba ještě pokrýt? - Střecha 7
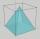 Střecha má tvar pravidelného čtyřbokého jehlanu s podstavnou hranou 12m a výškou 4m. Kolik procent připadlo na záhyby a odpad, jestliže se spotřebovalo na jeji zhotovení 181,4m² plechu?
Střecha má tvar pravidelného čtyřbokého jehlanu s podstavnou hranou 12m a výškou 4m. Kolik procent připadlo na záhyby a odpad, jestliže se spotřebovalo na jeji zhotovení 181,4m² plechu? - Čtyřboký hranol
 Výška pravidelného čtyřbokého hranolu je v = 10 cm, odchylka tělesových úhlopříčky od podstavy je 60°. Určete délku podstavových hran, povrch a objem kvádru.
Výška pravidelného čtyřbokého hranolu je v = 10 cm, odchylka tělesových úhlopříčky od podstavy je 60°. Určete délku podstavových hran, povrch a objem kvádru. - Stříška 2
 Kolik plechu je třeba na stříšku, která má tvar pravidelného čtyřbokého jehlanu, jestliže její hrana je dlouhá 2,8 m a výška stříšky je 0,8 m. Počítej 10 % na překryv ( navíc).
Kolik plechu je třeba na stříšku, která má tvar pravidelného čtyřbokého jehlanu, jestliže její hrana je dlouhá 2,8 m a výška stříšky je 0,8 m. Počítej 10 % na překryv ( navíc). - Komolý kruhový kužel
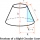 Betonový podstavec má tvar pravoúhlého komolého kruhového kužele s výškou 2,5 metru. Průměr horní a dolní základny je 3 stopy a 5 stop. Určitě boční plochu povrchu, celkovou plochu povrchu a objem podstavce.
Betonový podstavec má tvar pravoúhlého komolého kruhového kužele s výškou 2,5 metru. Průměr horní a dolní základny je 3 stopy a 5 stop. Určitě boční plochu povrchu, celkovou plochu povrchu a objem podstavce. - Věž
 Kolik metrů čtverečních je potřeba na pokrytí věže tvaru pravidelného čtyřbokého jehlanu o podstavné hraně 10 metrů, je-li odchylka boční hrany od roviny podstavy 68°? Při pokrytí se počítá s odpadem 10%.
Kolik metrů čtverečních je potřeba na pokrytí věže tvaru pravidelného čtyřbokého jehlanu o podstavné hraně 10 metrů, je-li odchylka boční hrany od roviny podstavy 68°? Při pokrytí se počítá s odpadem 10%. - Plášť = 2 x podstava
 Pravidelný čtyřboký hranol má objem 864cm³ a obsah jeho pláště je dvojnásobkem obsahu jeho podstavy. Určete velikost jeho tělesové úhlopříčky.
Pravidelný čtyřboký hranol má objem 864cm³ a obsah jeho pláště je dvojnásobkem obsahu jeho podstavy. Určete velikost jeho tělesové úhlopříčky. - Vypočtěte
 Vypočtěte povrch a objem pravidelného čtyřstěnu vysokého 4,9 cm, jehož hrana podstavy má délku 6 cm
Vypočtěte povrch a objem pravidelného čtyřstěnu vysokého 4,9 cm, jehož hrana podstavy má délku 6 cm - Vypočítejte 7638
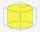 Do válce o výšce 10 centimetrů je vložen kvádr se čtvercovou podstavou tak, že jeho podstavava je vepsána do podstavy válce. Hrana podstavy kvádru měří 4 cm. Obě tělesa mají stejnou výšku. Vypočítejte rozdíl objemů válce a kvádru
Do válce o výšce 10 centimetrů je vložen kvádr se čtvercovou podstavou tak, že jeho podstavava je vepsána do podstavy válce. Hrana podstavy kvádru měří 4 cm. Obě tělesa mají stejnou výšku. Vypočítejte rozdíl objemů válce a kvádru - Kostolní střecha
 Střecha na budově je kužel s výškou 3 metry a poloměrem, který se rovná polovině výšky střechy. Kolik m² střechy nám třeba opravit, pokud se při bouři poškodilo 20%?
Střecha na budově je kužel s výškou 3 metry a poloměrem, který se rovná polovině výšky střechy. Kolik m² střechy nám třeba opravit, pokud se při bouři poškodilo 20%? - Těžítko 3
 Těžítko ze skla má tvar pravidelného čtyřbokého jehlanu o hraně podstavy 10cm. Stěny pláště jsou rovnostranné trojúhelníky. Jakou hmotnost v gramech má těžítko, jestliže hustota skla je 2500kg/m³?
Těžítko ze skla má tvar pravidelného čtyřbokého jehlanu o hraně podstavy 10cm. Stěny pláště jsou rovnostranné trojúhelníky. Jakou hmotnost v gramech má těžítko, jestliže hustota skla je 2500kg/m³? - Obvod 34
 Obvod podstavy pravidelného čtyřbokého jehlanu je stejně velký jako jeho výška. Jehlan má objem 288 dm³. Vypočítejte jeho povrch. Výsledek zaokrouhlete na celé dm².
Obvod podstavy pravidelného čtyřbokého jehlanu je stejně velký jako jeho výška. Jehlan má objem 288 dm³. Vypočítejte jeho povrch. Výsledek zaokrouhlete na celé dm². - Slunečník
 Slunečník má tvar pláště šestibokého pravidelného jehlanu, jehož podstavná hrana a=6dm a výška v=25cm. Kolik látky je třeba na zhotovení slunečníku, počítáme-li na spoje a odpad 10%.
Slunečník má tvar pláště šestibokého pravidelného jehlanu, jehož podstavná hrana a=6dm a výška v=25cm. Kolik látky je třeba na zhotovení slunečníku, počítáme-li na spoje a odpad 10%. - Trojboký hranol
 Podstava kolmého trojbokého hranolu je pravoúhlý trojúhelník, jehož přepona je 10cm a jedna odvěsna 8cm. Výška hranolu je 75% z obvodu podstavy. Vypočtěte objem a povrch hranolu.
Podstava kolmého trojbokého hranolu je pravoúhlý trojúhelník, jehož přepona je 10cm a jedna odvěsna 8cm. Výška hranolu je 75% z obvodu podstavy. Vypočtěte objem a povrch hranolu. - Láhve džusu
 Kolik dvoulitrových lahví džusu potřebujeme koupit, pokud ho chceme přelít do 50 džbánů tvaru rotačního kužele s průměrem podstavy 24 cm a stranou délky 1,5 dm.
Kolik dvoulitrových lahví džusu potřebujeme koupit, pokud ho chceme přelít do 50 džbánů tvaru rotačního kužele s průměrem podstavy 24 cm a stranou délky 1,5 dm.
Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
