Stereometrie - slovní úlohy a příklady - strana 95 z 119
Počet nalezených příkladů: 2379
- Koule 25
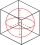 Koule o průměru 10 cm je v krabičce tvaru krychle o hraně 10cm. Kolik procent krabičky koule vyplňuje?
Koule o průměru 10 cm je v krabičce tvaru krychle o hraně 10cm. Kolik procent krabičky koule vyplňuje? - Trojitý poměr
 Objem kostky a kvádru je v poměru 3:2. Objem koule a kvádru je v poměru 1:3. V jakém poměru jsou objemy kostky, kvádru a koule?
Objem kostky a kvádru je v poměru 3:2. Objem koule a kvádru je v poměru 1:3. V jakém poměru jsou objemy kostky, kvádru a koule? - Dvojnásob cm
 Jeden rozměr kvádru zvětšíme dvojnásob a druhý zmenšíme o třetinu. Jak se změní jeho objem.
Jeden rozměr kvádru zvětšíme dvojnásob a druhý zmenšíme o třetinu. Jak se změní jeho objem. - Povrch a hrana
 Hrana kostky, jejíž objem je 58,3% jejího povrchu je: a) 3,5cm b) 4,5cm c) 2,5cm d) 1,5cm
Hrana kostky, jejíž objem je 58,3% jejího povrchu je: a) 3,5cm b) 4,5cm c) 2,5cm d) 1,5cm - Chodník 2
 Na chodník 3m široký a 8m dlouhý se spotřebovalo 2m³ mosaikového kamene (žulových kostek). Mistr dlaždičský měl vydlaždit chodník 2,5m široký a 65m dlouhý. Kolik m³ kamene spotřebuje?
Na chodník 3m široký a 8m dlouhý se spotřebovalo 2m³ mosaikového kamene (žulových kostek). Mistr dlaždičský měl vydlaždit chodník 2,5m široký a 65m dlouhý. Kolik m³ kamene spotřebuje? - Ledové kostky
 Sochař skládá ledové město z kostek ledu. Kostka o délce hrany 2 dm má hmotnost 7,2 kg. O kolik kilogramů je od ní ledová kostka o délce hrany 6 dm těžší?
Sochař skládá ledové město z kostek ledu. Kostka o délce hrany 2 dm má hmotnost 7,2 kg. O kolik kilogramů je od ní ledová kostka o délce hrany 6 dm těžší? - Autobusová
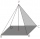 Autobusová čekárna má tvar pravidelného čtyřbokého jehlanu vysokého 4 m s hranou podstavy o velikosti 5 m. Vypočítejte, kolik m² střešní krytiny je třeba na pokrytí tří stěn pláště, bereme-li v úvahu 40% krytiny navíc na překrytí.
Autobusová čekárna má tvar pravidelného čtyřbokého jehlanu vysokého 4 m s hranou podstavy o velikosti 5 m. Vypočítejte, kolik m² střešní krytiny je třeba na pokrytí tří stěn pláště, bereme-li v úvahu 40% krytiny navíc na překrytí. - Hrana krychle
 Určete hranu krychle, jestliže její povrch se rovná 37,5 centimetrů čtverečních.
Určete hranu krychle, jestliže její povrch se rovná 37,5 centimetrů čtverečních. - Plocha stanu
 Vypočítejte, kolik plátna (bez podlahy) se spotřebuje na zhotovení stanu, který má tvar pravidelného čtyřbokého jehlanu. Hrana podstavy má délku 3 m a výška stanu je 2m.
Vypočítejte, kolik plátna (bez podlahy) se spotřebuje na zhotovení stanu, který má tvar pravidelného čtyřbokého jehlanu. Hrana podstavy má délku 3 m a výška stanu je 2m. - Jednociferné délky
 Dvě kostky vymodelované z plastelíny mají jednociferné celočíselné délky hran s rozdílem 1cm. Dá se z téhož množství plastelíny vymodelovat jedna velká kostka s celočíselnou délkou hrany?
Dvě kostky vymodelované z plastelíny mají jednociferné celočíselné délky hran s rozdílem 1cm. Dá se z téhož množství plastelíny vymodelovat jedna velká kostka s celočíselnou délkou hrany? - Místnost
 Místnost má tvar kvádru o rozměrech: délka 50m a šířka 60dm a vyška 300cm. Vypočítejte, kolik bude stat vybělení této místnosti (podlaha se nevyběluje), pokud plocha oken a dveří je 15% z celkové plochy a za 1m² se plati 15 eur.
Místnost má tvar kvádru o rozměrech: délka 50m a šířka 60dm a vyška 300cm. Vypočítejte, kolik bude stat vybělení této místnosti (podlaha se nevyběluje), pokud plocha oken a dveří je 15% z celkové plochy a za 1m² se plati 15 eur. - Žebřík
 4m žebřík se dotýká krychle 1mx1m postavené u zdi. Jak vysoko na zdi dosáhne?
4m žebřík se dotýká krychle 1mx1m postavené u zdi. Jak vysoko na zdi dosáhne? - Odsek úseče
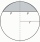 Od koule k o poloměru r=1 je odseknuta taková úseč, že objem koule vepsané do této úseče je roven 1/6 objemu úseče. Jaká je vzdálenost sečné roviny od středu koule k?
Od koule k o poloměru r=1 je odseknuta taková úseč, že objem koule vepsané do této úseče je roven 1/6 objemu úseče. Jaká je vzdálenost sečné roviny od středu koule k? - Archimedes - vor
 Chci postavit vor, mám trámy o čtvercovém průřezu se stranou a=20cm a délce l=2m, hustota dřeva 670 kg/m³, spojím 10 trámů-jaký je objem voru a jeho hmotnost? Do jaké hloubky se vor potopí na vodě ( hustota vody 1000kg/m³ )? Hmotnost jednoho člověka je 50
Chci postavit vor, mám trámy o čtvercovém průřezu se stranou a=20cm a délce l=2m, hustota dřeva 670 kg/m³, spojím 10 trámů-jaký je objem voru a jeho hmotnost? Do jaké hloubky se vor potopí na vodě ( hustota vody 1000kg/m³ )? Hmotnost jednoho člověka je 50 - Tesař
 Z dřevěného kvádru tesař odřízl menší kvádr s polovičními délkami hran. Kolik procent dřeva uřízl?
Z dřevěného kvádru tesař odřízl menší kvádr s polovičními délkami hran. Kolik procent dřeva uřízl? - Sud 3
 Sud s vodou má hmotnost 118 kg. Když z něj odlijeme 75% vody, bude mať hmotnost 35kg. Kolik kg připadá na prázdný sud?
Sud s vodou má hmotnost 118 kg. Když z něj odlijeme 75% vody, bude mať hmotnost 35kg. Kolik kg připadá na prázdný sud? - Drevina smrk
 Na vagón o ložné šířce 2 700 mm je pečlivě naložena a do 9 vrstev poskládána smrková kulatina o průměru 270 mm a délce 4 m. Kolik váží takovýto náklad smrkového dřeva je-li jeho hustota 700 kg/m³?
Na vagón o ložné šířce 2 700 mm je pečlivě naložena a do 9 vrstev poskládána smrková kulatina o průměru 270 mm a délce 4 m. Kolik váží takovýto náklad smrkového dřeva je-li jeho hustota 700 kg/m³? - Hranol a kostka
 Hranol se čtvercovou podstavou a=25cm, výška h=45cm. kostka: b=15cm a) kolik procent z objemu hranolu tvoří objem kostky? b) jakou výšku by měl mít hranol, aby měl stejný objem jako kostka?
Hranol se čtvercovou podstavou a=25cm, výška h=45cm. kostka: b=15cm a) kolik procent z objemu hranolu tvoří objem kostky? b) jakou výšku by měl mít hranol, aby měl stejný objem jako kostka? - Krychle 41
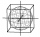 Krychle o hraně a je zbroušena na kouli o co největším objemu. Urči, kolik % činil odpad z broušení.
Krychle o hraně a je zbroušena na kouli o co největším objemu. Urči, kolik % činil odpad z broušení. - Povrch kostky
 Povrch kostky byl původně 216 centimetrů čtverečních. Povrch kostky se zmenšil z 216 na 54 centimetrů čtverečních. Vypočtěte, o kolik % se zmenšila hrana kostky.
Povrch kostky byl původně 216 centimetrů čtverečních. Povrch kostky se zmenšil z 216 na 54 centimetrů čtverečních. Vypočtěte, o kolik % se zmenšila hrana kostky.
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
