Trojúhelník + válec - příklady a úlohy

Počet nalezených příkladů: 22

Na válec
Na válec o průměru 4,6 cm nasaďte část koule tak, aby povrch této části byl 20 cm². Určete r koule ze které byl vrchlík seříznut.
Do odměrného
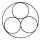Do odměrného válce o vnitřním průměru 10 cm jsou uloženy 4 kovové koule o průměru 5 cm. Jaké nejmenší množství vody je třeba do válce nalít, aby všecky 4 koule byly pod hladinou?
Dvě koule
Dvě koule, jedna s poloměrem 8 cm a další s poloměrem 6 cm, se vloži do válcové plastové nádoby s poloměrem 10 cm. Najděte množství vody potřebné k jejich potopení.
Valec naležato
Válec o průměru 3m a výšce/délce 15 m je položen naležato. Je do něj napuštěna voda, která sahá do výšky 60 cm pod osu válce. Kolik hektolitrů vody je ve válci?
Věz vysílače
Věz vysílače je v 80 metrech výšky stabilizována k zemi 4 ocelovými lany ukotvenými v zemi 60 metrů od paty věže. Vypočítejte, kolik metrů ocelového lana bylo potřeba ke stabilizaci vysílací věže. Použité ocelové lano má kruhový průřez o poloměru 2 cm. Vy
Kužel s průměrem
Nádoba tvaru kužele s průměrem dna 60cm a boční stranou délky 0,5m je zcela naplněna vodou. Vodu přelijeme do nádoby, která má tvář válce o poloměru 3dm a výšce 20cm. Bude válec přetékat, nebo naopak nebude plný? Vypočítejte kolik vody přeteče, nebo naopa
Tajný poklad
Skauti mají stan ve tvaru pravidelného čtyřbokého jehlanu se stranou podstavy 4 m a výšce 3 m. Do stanu potřebují schovat válcovou nádobu s tajným pokladem. Určete poloměr r (a výšku h) nádoby tak, aby mohli schovat co nejobjemnější poklad.
Válec
Válec je třikrát vyšší než je jeho šířka. Délka úhlopříčky válce je 20 cm. Najděte plochu horní části válce.
Plovoucí sud
Na vodě plave sud tvaru válce, a to tak že z vody vyčnívá 8 dm do výšky a na hladině má šířku 23 dm. Délka sudu je 24 dm. Vypočítejte objem sudu.
Kruhový bazén
Podstava bazénu má tvar kruhu o poloměru r = 10m kromě kruhového odstavce, který určuje tětiva délky 10m. Jeho hloubka je h = 2m. Kolik hektolitrů vody se vejde do bazénu?
Plášť 8
Plášť kužele je vytvořen svinutím kruhové úseče o poloměru 1. Pro jaký středový úhel dané kruhové výseče bude objem vzniklého kužele maximální?
Rotační telesa
Rotační kužel a rotační válec mají stejný objem 180 cm³ a stejnou výšku v=15cm. Které z těchto dvou těles má větší povrch?
Šestihran
Pravidelný šestihran (6 úhelník) se stěnou 6 cm je otočen o 60 ° podél přímky procházející její nejdelší úhlopříčce. Jaký je objem takto vytvořeného tělesa?
Válec horizontálně
Kolik nafty je ve vodorovné nádrži ve tvaru válce o délce 10m, když šířka hladiny je 1m a hladina je 0,2m pod horní stranou válce?
Borovice
Z kmene borovice dlouhé 6m a průměru 35cm se má vyřezat trám s příčným řezem ve tvaru čtverce tak, aby čtverec měl co největší obsah. Vypočítej délku strany čtverce. Vypočítej objem trámu v metrech krychlových.
Pravítko
Na pravítko, které má tvar hranolu s podstavou tvaru rovnostranného trojúhelníku o straně délky 3 cm, se má vyrobit pouzdro tvaru válce. Jaký musí být nejmenší vnitřní průměr pouzdra? Rozměr určete s přesností na desetiny centimetru
Špejle
Sklenice má tvar válce s vnitřním průměrem 12 cm, výška sklenice ode dna je 16 cm. Seříznutou špejli lze šikmo vložit do sklenice tak, že nepřečnívá přes okraj. Jaká je největší možná délka seříznuté špejle? (Tloušťka špejle se při výpočtu zanedbává.)
Válec 17
V rotačním válci je dáno: V= 120 cm³, v=4 cm. Vypočtětě r, S plášte.
Vypočítejte 9
Vypočítejte objem a povrch válce, jehož osový řez je obdélník široký 15 cm s úhlopříčkou dlouhou 25 cm.
Válec a krychle
Určete obsah pláště a objem rotačního válce, který je opsán krychli s hranou délky 5 cm.

Máš zajímavý příklad nebo úlohu, který nevíš vypočítat? Vlož úlohu a my Ti ju zkusíme vypočítat.

Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku. Příklady na trojúhelník. Příklady na válec.