MO Z6 I-3 2017 sklenice
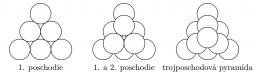
Honza měl 100 stejných zavařovacích sklenic, z kterých si stavěl trojboké pyramidy. Nejvyšší poschodí pyramidy má vždy jednu sklenici, druhé poschodí shora představuje rovnostranný trojúhelník, jehož strana sestává ze dvou sklenic, atd. Příklad konstrukce
trojposchoďové pyramidy je na obrázku.
1. Kolik sklenic Honza potřeboval na pětiposchoďovou pyramidu?
2. Kolik poschodí měla pyramida, na niž bylo použito co nejvíc Honzových sklenic?
trojposchoďové pyramidy je na obrázku.
1. Kolik sklenic Honza potřeboval na pětiposchoďovou pyramidu?
2. Kolik poschodí měla pyramida, na niž bylo použito co nejvíc Honzových sklenic?
Správná odpověď:
Tipy na související online kalkulačky
Vypočet rovnostranného trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Prarodičů 7287
 Starý otec si na spoření vyčlenil 1200 €. Vždy na zač. Měsíce vložil do banky 100 € při úrokové míře 3%p. A. Na konci roku měl v bance 1219,68 €. Babička dala hned celou částku 1200 € do banky za stejných podmínek jako dědeček. a. ) kolik měla po roce na
Starý otec si na spoření vyčlenil 1200 €. Vždy na zač. Měsíce vložil do banky 100 € při úrokové míře 3%p. A. Na konci roku měl v bance 1219,68 €. Babička dala hned celou částku 1200 € do banky za stejných podmínek jako dědeček. a. ) kolik měla po roce na - Partiích 2711
 Honza se rád hraje různé hry o fazolky. Nedávno si zahrál s Petrem dvě partie. V první partii vyhrál 32 fazolek, ve druhé partii prohrál 75 fazolek. Jak byl Honza na tom po těchto dvou partiích? Měl více nebo méně fazolek než na začátku? a teď zjisti o ko
Honza se rád hraje různé hry o fazolky. Nedávno si zahrál s Petrem dvě partie. V první partii vyhrál 32 fazolek, ve druhé partii prohrál 75 fazolek. Jak byl Honza na tom po těchto dvou partiích? Měl více nebo méně fazolek než na začátku? a teď zjisti o ko - Cukr - kvádr
 Pejko dostal od svého pána kvádr složený z navzájem stejných kostek cukru, kterých bylo nejméně 1000 a nejvíce 2000. Pejko kostky cukru odjeda po jednotlivých vrstvách-první den odjedu jednu vrstvu zepředu, druhý den jednu vrstvu zprava a třetí den jednu
Pejko dostal od svého pána kvádr složený z navzájem stejných kostek cukru, kterých bylo nejméně 1000 a nejvíce 2000. Pejko kostky cukru odjeda po jednotlivých vrstvách-první den odjedu jednu vrstvu zepředu, druhý den jednu vrstvu zprava a třetí den jednu - Plot 4
 Na tři stejné díly plotu přibil tatínek 54 tyček. Kolik tyček potřeboval celkem na plot, který měl 10 stejných dílů a branku, na kterou spotřeboval tatínek ještě 10 tyček?
Na tři stejné díly plotu přibil tatínek 54 tyček. Kolik tyček potřeboval celkem na plot, který měl 10 stejných dílů a branku, na kterou spotřeboval tatínek ještě 10 tyček?
- Zvláštní hodinky
 Fero si na bleším trhu koupil zvláštní hodinky. Mají jen jednu ručičku (minutovou) a číselník, na kterém se zobrazuje, jaký úhel by právě svírala hodinová a minutová ručička. Kolik bylo hodin, kdy se na jeho hodinkách objevilo to, co vidíš na obrázku - mi
Fero si na bleším trhu koupil zvláštní hodinky. Mají jen jednu ručičku (minutovou) a číselník, na kterém se zobrazuje, jaký úhel by právě svírala hodinová a minutová ručička. Kolik bylo hodin, kdy se na jeho hodinkách objevilo to, co vidíš na obrázku - mi - Pyramidy
 Jaký je úhel mezi stěnami a základnou trojboké pyramidy, jejíž strany jsou stejné?
Jaký je úhel mezi stěnami a základnou trojboké pyramidy, jejíž strany jsou stejné? - Kuličky 8
 Petr si vybral kuličky dvou barev. Kolik kterých měl jestliže počty žlutých a červených byly v poměru 7 : 5 a žlutých bylo o šest více?
Petr si vybral kuličky dvou barev. Kolik kterých měl jestliže počty žlutých a červených byly v poměru 7 : 5 a žlutých bylo o šest více? - Z9–I–4 MO 2017
 Čísla 1, 2, 3, 4, 5, 6, 7, 8 a 9 se chystala na cestu vlakem se třemi vagóny. Chtěla se rozsadit tak, aby v každém vagóně seděla tři čísla a největší z každé trojice bylo rovno součtu zbylých dvou. Průvodčí tvrdil, že to není problém, a snažil se číslům p
Čísla 1, 2, 3, 4, 5, 6, 7, 8 a 9 se chystala na cestu vlakem se třemi vagóny. Chtěla se rozsadit tak, aby v každém vagóně seděla tři čísla a největší z každé trojice bylo rovno součtu zbylých dvou. Průvodčí tvrdil, že to není problém, a snažil se číslům p - Součet obsahů
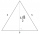 Nád výškou rovnostranného trojúhelníku ABC je sestrojen rovnostranný trojúhelník A1, B1, C1, nad jeho výškou je sestrojen rovnostranný trojúhelník A2, B2, C2, atd. Se postup neustále opakuje. Jaký je velký součet obsahů všech trojúhelníků, pokud strana tr
Nád výškou rovnostranného trojúhelníku ABC je sestrojen rovnostranný trojúhelník A1, B1, C1, nad jeho výškou je sestrojen rovnostranný trojúhelník A2, B2, C2, atd. Se postup neustále opakuje. Jaký je velký součet obsahů všech trojúhelníků, pokud strana tr
- Žebřík šikmej
 Spodní příčka žebříku je dlouhá 36 palců a nejvyšší příčka má délku 24 palců. Pokud má žebřík 18 příček, o kolik palců je každá další příčka kratší než příčka pod ním. Kolik stop (ft) dřeva bylo použito na výrobu příček?
Spodní příčka žebříku je dlouhá 36 palců a nejvyšší příčka má délku 24 palců. Pokud má žebřík 18 příček, o kolik palců je každá další příčka kratší než příčka pod ním. Kolik stop (ft) dřeva bylo použito na výrobu příček? - Pyramida v Gize
 Velká pyramida v Gize má tvar pravidelného čtyřbokého jehlanu. Podstavná hrana má délku 227 m a výška pyramidy je 140 m. Jakou hmotnost má kámen, který byl potřebný na stavbu této pyramidy, pokud hmotnost 1 m³ kamene je 2,5 t?
Velká pyramida v Gize má tvar pravidelného čtyřbokého jehlanu. Podstavná hrana má délku 227 m a výška pyramidy je 140 m. Jakou hmotnost má kámen, který byl potřebný na stavbu této pyramidy, pokud hmotnost 1 m³ kamene je 2,5 t? - Očislovení 71274
 Na očislovení hrubé knihy bylo použito 1533 číslic. Kolik stran má tato kniha, je-li ocislována každá strana včetně strany 1?
Na očislovení hrubé knihy bylo použito 1533 číslic. Kolik stran má tato kniha, je-li ocislována každá strana včetně strany 1? - Pyramida
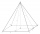 Najděte celkový povrch obdélníkové pyramidy, má-li je vysoká 8 dm a základna je 10 dm x 6 dm.
Najděte celkový povrch obdélníkové pyramidy, má-li je vysoká 8 dm a základna je 10 dm x 6 dm. - Pravidelného 44981
 Největší egyptská pyramida má tvar pravidelného čtyřbokého jehlanu s hranou podstavy přibližně 227 metrů a výškou asi 140 metrů. Kolik tun kamene přepravili dělníci na její stavbu? 1 kubík kamene má hmotnost 2 500 kg a chodby a místnosti uvnitř pyramidy z
Největší egyptská pyramida má tvar pravidelného čtyřbokého jehlanu s hranou podstavy přibližně 227 metrů a výškou asi 140 metrů. Kolik tun kamene přepravili dělníci na její stavbu? 1 kubík kamene má hmotnost 2 500 kg a chodby a místnosti uvnitř pyramidy z
- Plot
 Na 3 stejne díly plotu přibil tatinek 54 tyček. Kolik tyček potřeboval celkem na plot, ktery měl 10 stejnych dílů a branku, na kterou spotřeboval ješte 10 tyček?
Na 3 stejne díly plotu přibil tatinek 54 tyček. Kolik tyček potřeboval celkem na plot, ktery měl 10 stejnych dílů a branku, na kterou spotřeboval ješte 10 tyček? - Tablo
 Vaše třída vymyslí originální tablo-pyramida z fotek. Jaké minimální rozměry bude muset mít, když tam chcete umístit 50 fotek formátu 9x13. Chcete klasickou pyramidu, tzn. Každá další řada o jednu fotku méně, ale v poslední řadě dvě fotky (třídní a paní ř
Vaše třída vymyslí originální tablo-pyramida z fotek. Jaké minimální rozměry bude muset mít, když tam chcete umístit 50 fotek formátu 9x13. Chcete klasickou pyramidu, tzn. Každá další řada o jednu fotku méně, ale v poslední řadě dvě fotky (třídní a paní ř - Rozdělíme 6677
 Jak budeme volat jednu část, když celek rozdělíme na 5(6,7,8,9,10) stejných částí?
Jak budeme volat jednu část, když celek rozdělíme na 5(6,7,8,9,10) stejných částí?
