Naklonená rovina
Na naklonenú rovinu s uhlom sklonu 30° položím teleso (hmotný bod) s hmotnosťou 4 kg. Urči s akým zrýchlením sa teleso na naklonenej rovine pohybuje.
Správna odpoveď:
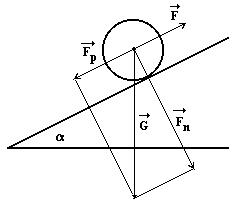
Tipy na súvisiace online kalkulačky
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
geometriaplanimetriagoniometria a trigonometriaJednotky fyzikálnych veličíntémaÚroveň náročnosti úlohy
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Teleso, trenie
 Teleso sa šmýka dolu po naklonenej rovine zvierajúcej s vodorovnou rovinou uhol α=π/4=45° za účinku síl trenia so zrýchlením a = 2,4 m/s². Pod akým uhlom β musí byť naklonená rovina, aby sa teleso po nej šmýkalo po malom postrčení konštantnou rýchlosťou?
Teleso sa šmýka dolu po naklonenej rovine zvierajúcej s vodorovnou rovinou uhol α=π/4=45° za účinku síl trenia so zrýchlením a = 2,4 m/s². Pod akým uhlom β musí byť naklonená rovina, aby sa teleso po nej šmýkalo po malom postrčení konštantnou rýchlosťou? - Naklonená rovina 2
 1. Akú veľkú prácu W musíme vykonať, aby sme vytiahli teleso o hmotnosti 200kg po naklonenej rovine o dĺžke 4m do celkovej výšky 1,5m. 2. Určite tiež silu, ktorú na to potrebujeme vyvinúť, ak zanedbáme odpor trenia. 3. Určite silu, ktorú by sme potreboval
1. Akú veľkú prácu W musíme vykonať, aby sme vytiahli teleso o hmotnosti 200kg po naklonenej rovine o dĺžke 4m do celkovej výšky 1,5m. 2. Určite tiež silu, ktorú na to potrebujeme vyvinúť, ak zanedbáme odpor trenia. 3. Určite silu, ktorú by sme potreboval - Zrýchlenie guličky
 Guľôčka, ktorú položíme na naklonenú rovinu, sa začne pohybovať a za dobu 5 s dosiahne rýchlosť 1 m/s. Za predpokladu, že pohyb guličky je rovnomerne zrýchlený, určite veľkosť jej zrýchlenia a dráhu, ktorú za uvedený čas prejde.
Guľôčka, ktorú položíme na naklonenú rovinu, sa začne pohybovať a za dobu 5 s dosiahne rýchlosť 1 m/s. Za predpokladu, že pohyb guličky je rovnomerne zrýchlený, určite veľkosť jej zrýchlenia a dráhu, ktorú za uvedený čas prejde. - Naklonená rovina
 Teleso spočíva na naklonenej rovine a pôsobí na nej tlakovou silou s veľkosťou 70N. Určte aký uhol zviera naklonená rovina s horizontálnou rovinou ak na teleso pôsobí tiažová sila s veľkosťou 100N.
Teleso spočíva na naklonenej rovine a pôsobí na nej tlakovou silou s veľkosťou 70N. Určte aký uhol zviera naklonená rovina s horizontálnou rovinou ak na teleso pôsobí tiažová sila s veľkosťou 100N. - Pohyb po kružnici
 Hmotný bod sa pohybuje rovnomerne po kružnici s polomerom r=2,7 m uhlovou rýchlosťou ω= 3,3 rad/s. Vypočítajte periódu, frekvenciu a dostredivé zrýchlenie tohto pohybu.
Hmotný bod sa pohybuje rovnomerne po kružnici s polomerom r=2,7 m uhlovou rýchlosťou ω= 3,3 rad/s. Vypočítajte periódu, frekvenciu a dostredivé zrýchlenie tohto pohybu. - Hmotný bod
 Na hmotný bod pôsobia dve rovnaké sily o veľkosti 30 N. Určte veľkosť výslednice, ak tieto sily zvierajú uhol 42°.
Na hmotný bod pôsobia dve rovnaké sily o veľkosti 30 N. Určte veľkosť výslednice, ak tieto sily zvierajú uhol 42°. - Voľný pád urýchlený
 Teleso o hmotnosti 5 kg sa pohybuje v zvislom smere nadol so zrýchlením a= 12 m/s² Aká sila okrem jeho tiaže naň pôsobí?
Teleso o hmotnosti 5 kg sa pohybuje v zvislom smere nadol so zrýchlením a= 12 m/s² Aká sila okrem jeho tiaže naň pôsobí?
