Lichobežník
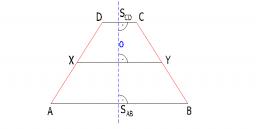
Daný je lichobežník ABCD so základňami AB, CD. Nech K je stred strany AB a L je stred strany CD. Obsah trojuholníka ALB je 15 cm2 a obsah trojuholníka DKC je 10 cm2. Vypočítajte obsah lichobežníka ABCD.
Vaša odpoveď:
Vaša odpoveď:
Zobrazujem 1 komentár:
Žiak
staci si uvedomit ze obsah dvoch casti ktore vzniknu ked dame do lichobezniku jeden z trojuholnikov su vlastne dohromady take velke ako ten druhy trojuholnik
Tipy na súvisiace online kalkulačky
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
planimetriazákladné operácie a pojmyÚroveň náročnosti úlohy
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Trojuholnik ABP
Je daný rovnoramenný lichobežník ABCD. Dĺžka strany AB je 10 cm, dĺžka CD je 7 cm, výška na AB je 4 cm. Bod P je päta výšky na stranu AD. Vypočítajte obsah trojuholníka ABP. - RR lichobeznik
Je daný rovnoramenný lichobežník ABCD so základňami |AB| = 36 m, |CD| = 200 dm a |BC| = 10 m . Vypočítajte obsah a obvod lichobežníka a dĺžku uhlopriečky AC - Pravouhlý lichobežník
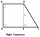Pravouhlý lichobežník ABCD so základňami AB a CD je rozdelený uhlopriečkou AC na dva rovnoramené pravouhlé trojuholníky. Dĺžka uhlopriečky AC je rovná 62 cm. Vypočítajte v cm štvorcových obsah lichobežníka a vypočítajte, o koľko cm sa líšia obvody trojuho - Urč obsah
Urč obsah lichobežníka ABCD, v ktorom platí: AB= 6 cm, Obsah trojuholníka ABC= 15 cm2, obsah trojuholníka BCD= 20 cm2, AB||CD. - Daný je 7 Daný je rovnoramenný lichobežník ABCD so základňami 10 cm a 14 cm. Výška lichobežníka je 6 cm. Určte vnútorné uhly lichobežníka.
- Dokážte
Lichobežník ABCD so základňami AB=a, CD=c má výšku v. Bod S je stred ramena BC. Dokážte že obsah trojuholníka ASD sa rovná polovici obsahu lichobežníka ABCD. - Štvoruholník ASBE
Na obrázku je štvorec ABCD so stredom S a stranou dlhou 8 cm. Bod E je l'ubovoľný bod strany CD rozny od C a D. Vypočítajte obsah štvoruholníka ASBE v cm².
