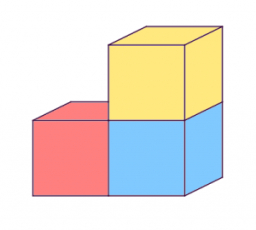
Hranol 38
Hranol so štvorcovou podstavou a=25cm, výška h=45cm. kocka: b=15cm
a) koľko percent z objemu hranola tvorí objem kocky?
b) akú výšku by mal mať hranol, aby mal taky istý objem ako kocka?
a) koľko percent z objemu hranola tvorí objem kocky?
b) akú výšku by mal mať hranol, aby mal taky istý objem ako kocka?
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Naša kalkulačka na výpočet percent Vám pomôže rýchlo vypočítať rôzne typické úlohy s percentami.
Tip: premeniť jednotky objemu vám pomôže naša kalkulačka premeny jednotiek objemu.
Tip: premeniť jednotky objemu vám pomôže naša kalkulačka premeny jednotiek objemu.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Hranol
 Kolmý hranol, ktorého podstavou je pravouhlý trojuholník s odvesnou dĺžky a = 8 cm a preponou c = 17 cm, má rovnaký objem ako kocka s hranou dĺžky 2 dm. a) Určte výšku hranola b) Vypočítajte povrch hranola c) Koľko percent povrchu kocky je povrch hranola
Kolmý hranol, ktorého podstavou je pravouhlý trojuholník s odvesnou dĺžky a = 8 cm a preponou c = 17 cm, má rovnaký objem ako kocka s hranou dĺžky 2 dm. a) Určte výšku hranola b) Vypočítajte povrch hranola c) Koľko percent povrchu kocky je povrch hranola - Kocka v guli
 Kocka je vpísaná do gule s polomerom r=6 cm. Koľko percent tvorí objem kocky z objemu gule? Iné znenie príkladu: Do gule je vpísaná kocka so stranou dĺžky a. Vypočítajte, koľko percent objemu gule tvorí objem kocky.
Kocka je vpísaná do gule s polomerom r=6 cm. Koľko percent tvorí objem kocky z objemu gule? Iné znenie príkladu: Do gule je vpísaná kocka so stranou dĺžky a. Vypočítajte, koľko percent objemu gule tvorí objem kocky. - Hranol - litre
 Hranol so štvorcovou podstavou má objem 200 litrov, dĺžka jeho podstavnej hrany je a decimetrov. Zapíš výšku hranola zodpovedajúcim výrazom hranola v decimetroch.
Hranol so štvorcovou podstavou má objem 200 litrov, dĺžka jeho podstavnej hrany je a decimetrov. Zapíš výšku hranola zodpovedajúcim výrazom hranola v decimetroch. - Podstava 9
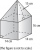 Podstava hranola má tvar štvorca so stranou 10 cm. Výška hranola je 20 cm. Vypočítajte výšku ihlana s podstavou tvaru štvorca so stranou 10 cm, ktorý má štyrikrát menší objem ako hranol.
Podstava hranola má tvar štvorca so stranou 10 cm. Výška hranola je 20 cm. Vypočítajte výšku ihlana s podstavou tvaru štvorca so stranou 10 cm, ktorý má štyrikrát menší objem ako hranol. - Podstava 10
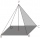 Podstava hranola má tvar štvorca so stranou 10 cm. Výška hranola je 20 cm. Vypočítajte výšku ihlana s podstavou tvaru štvorca so stranou 10 cm, ktorý má štyrikrát menší objem ako hranol.
Podstava hranola má tvar štvorca so stranou 10 cm. Výška hranola je 20 cm. Vypočítajte výšku ihlana s podstavou tvaru štvorca so stranou 10 cm, ktorý má štyrikrát menší objem ako hranol. - Mimozemská loď
 Mimozemská loď má tvar gule o polomere r = 3000m a jej posádka potrebuje loďou odviezť nazbieraný výskumný materiál v boxe v tvare kvádra so štvorcovou podstavou. Určte dĺžku podstavy a (a výšku h) tak, aby mal box najväčší možný objem.
Mimozemská loď má tvar gule o polomere r = 3000m a jej posádka potrebuje loďou odviezť nazbieraný výskumný materiál v boxe v tvare kvádra so štvorcovou podstavou. Určte dĺžku podstavy a (a výšku h) tak, aby mal box najväčší možný objem. - Hranol
 Z kocky s dĺžkou hrany 3 cm bol vyrezaný hranol s štvorcovou podstavou o obsahu 1 cm² a výškou 3 cm. Aký je povrch telesa, ktoré z kocky vzniklo po vyrezanie hranola?
Z kocky s dĺžkou hrany 3 cm bol vyrezaný hranol s štvorcovou podstavou o obsahu 1 cm² a výškou 3 cm. Aký je povrch telesa, ktoré z kocky vzniklo po vyrezanie hranola?
