Priesečníky
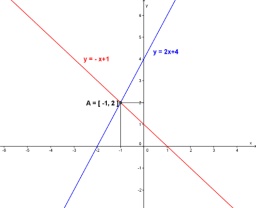
Určte priesečníky grafu funkcie sa súradnicovými osami:
f (x): y = x + 3/5
f (x): y = x + 3/5
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Téma:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Narysuj 13
 Narysuj graf funkcie danej rovnicou y = -2x +3, urč jej priesečníky so súradnicovými osami a doplň chýbajúce súradnice A[3;? ], B[? ;8].
Narysuj graf funkcie danej rovnicou y = -2x +3, urč jej priesečníky so súradnicovými osami a doplň chýbajúce súradnice A[3;? ], B[? ;8]. - Kde sa
 Kde sa nachádza priesečník funkcie y=-3x+ 5 so súradnicovými osami x a y? (kde sa nachádzu na osi x a osi y)
Kde sa nachádza priesečník funkcie y=-3x+ 5 so súradnicovými osami x a y? (kde sa nachádzu na osi x a osi y) - Priesečníky 62534
 Rovnica linearnou funkciou je : y=-3x+4 a) urči priesečníky s osami načrtni graf b) pre ktoré x platí f(x)=-1 c) pre ktoré x platí f(x)=0 d) pre ktoré y platí f(-1/2)=y
Rovnica linearnou funkciou je : y=-3x+4 a) urči priesečníky s osami načrtni graf b) pre ktoré x platí f(x)=-1 c) pre ktoré x platí f(x)=0 d) pre ktoré y platí f(-1/2)=y - Priesečníkov 80587
 Nakreslite graf funkcie y = -2x + 3 a vypočítajte súradnice priesečníkov grafu funkcie s osami x a y
Nakreslite graf funkcie y = -2x + 3 a vypočítajte súradnice priesečníkov grafu funkcie s osami x a y
- Priesečníky 2574
 Vypočítaj priesečníky s osami x a y funkcie h:y=4/5x-3
Vypočítaj priesečníky s osami x a y funkcie h:y=4/5x-3 - XY trojuholník
 Vypočítajte obsah trojuholníka, ktorý tvorí priamka 7x+8y-69=0 so súradnicovými osami.
Vypočítajte obsah trojuholníka, ktorý tvorí priamka 7x+8y-69=0 so súradnicovými osami. - Súradnice
 Určte obsah trojuholníka daného priamkou -7x + 7y + 63 = 0 a súradnicovými osi x a y.
Určte obsah trojuholníka daného priamkou -7x + 7y + 63 = 0 a súradnicovými osi x a y. - Priesečníky 25141
 Kvadratická funkcia má predpis y=x²-2x-3. Načrtnite graf tejto funkcie. Určite priesečníky s osami. Určite súradnice vrcholu.
Kvadratická funkcia má predpis y=x²-2x-3. Načrtnite graf tejto funkcie. Určite priesečníky s osami. Určite súradnice vrcholu. - Zapíš 5
 Zapíš či je funkcia rastúca alebo klesajúca a urči súradnice priesečníka s osami x a y: y=3x-2 y=5x+5 y=-0,5x-1
Zapíš či je funkcia rastúca alebo klesajúca a urči súradnice priesečníka s osami x a y: y=3x-2 y=5x+5 y=-0,5x-1
- Obvod trojuholníka 3
 Urči obvod trojuholníka ABC kde bod A je začiatok súradnicovej sústavy, bod B je priesečník grafu linearnej funkcie f: y = - 3/4• x + 3 s osou x a C je priesečník grafu tejto funkcie s osou y.
Urči obvod trojuholníka ABC kde bod A je začiatok súradnicovej sústavy, bod B je priesečník grafu linearnej funkcie f: y = - 3/4• x + 3 s osou x a C je priesečník grafu tejto funkcie s osou y. - Napíšte 7
 Napíšte rovnicu elipsy, ktorá prechádzada bodmi a jej osi sú totožné so súradnicovými osami, ked’: A = [2, 3] a B = [−1, −4].
Napíšte rovnicu elipsy, ktorá prechádzada bodmi a jej osi sú totožné so súradnicovými osami, ked’: A = [2, 3] a B = [−1, −4]. - Aký je 3
 Aký je súčet všetkých súradníc bodov, ktoré sú priesečníkmi priamky p: x = -1-2t, y = 5-4t, z = -3+6t, kde t je reálne číslo, so súradnicovými rovinami xy a yz?
Aký je súčet všetkých súradníc bodov, ktoré sú priesečníkmi priamky p: x = -1-2t, y = 5-4t, z = -3+6t, kde t je reálne číslo, so súradnicovými rovinami xy a yz? - Usporiadané 4649
 Urči päť riešení rovnice o dvoch neznámych. Zapíš ako usporiadané dvojice a zakresli do grafu. Ako vyzerá graf lineárnej rovnice? 2x+3y=7
Urči päť riešení rovnice o dvoch neznámych. Zapíš ako usporiadané dvojice a zakresli do grafu. Ako vyzerá graf lineárnej rovnice? 2x+3y=7 - Priesečníky 62784
 Je daná kvadratická funkcia: y=-x²+2x+3 a) urči priesečníky s osou x, y a vrchol V b) načrtni graf a popíš c) pre ktoré x platí f(x)=3
Je daná kvadratická funkcia: y=-x²+2x+3 a) urči priesečníky s osou x, y a vrchol V b) načrtni graf a popíš c) pre ktoré x platí f(x)=3
- Kvadratickej 44431
 1. V kartézskom rámci o funkciách f a g vieme, že: funkcia (f) je definovaná vzťahom f (x) = 2x², funkcia (g) je definovaná vzťahom g (x) = x + 3, bod (O) je začiatkom referencie, bod (C) je priesečník grafu funkcie (g ) s osou poradnice, body A a B sú pr
1. V kartézskom rámci o funkciách f a g vieme, že: funkcia (f) je definovaná vzťahom f (x) = 2x², funkcia (g) je definovaná vzťahom g (x) = x + 3, bod (O) je začiatkom referencie, bod (C) je priesečník grafu funkcie (g ) s osou poradnice, body A a B sú pr - Kružnica
 Kružnica k má stred S[-3; -10] a najväčšia tetiva má dĺžku 12. Koľko spoločných bodov má kružnica so súradnicovými osami?
Kružnica k má stred S[-3; -10] a najväčšia tetiva má dĺžku 12. Koľko spoločných bodov má kružnica so súradnicovými osami? - Priesečníky kružníc
 Nájdite priesečníky kružníc: x² + y² + 6 x - 10 y + 9 = 0 a x² + y² + 18 x + 4 y + 21 = 0
Nájdite priesečníky kružníc: x² + y² + 6 x - 10 y + 9 = 0 a x² + y² + 18 x + 4 y + 21 = 0
