Úhlopříčky

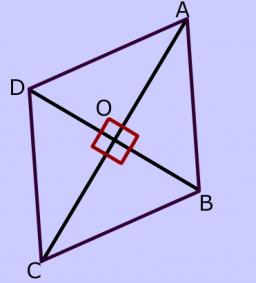
V kosočtverci je dáno a=160cm, alfa = 60 stupňů. Vypočtěte velikosti úhlopříček.

Správná odpověď:

u1 =  160 cm
u2 =  277,13 cm

Postup správného řešení:

a=160 cm α=60 ∘  u12​ = a2+a2−2aa cos α u12​ = 2a2−2a2 cos α u1​=a⋅ 2⋅ (1−cosα)​=a⋅ 2⋅ (1−cos60° )​=160⋅ 2⋅ (1−cos60° )​=160⋅ 2⋅ (1−0,5)​=160=160 cm
β=180−α=180−60=120 ∘ u22​ = a2+a2−2aa cos β u22​ = 2a2−2a2 cos β u2​=a⋅ 2⋅ (1−cosβ)​=a⋅ 2⋅ (1−cos120° )​=160⋅ 2⋅ (1−cos120° )​=160⋅ 2⋅ (1−(−0,5))​=277,13=277,13 cm

Zkusit jiný příklad


Našel jsi chybu či nepřesnost? Klidně nám ji napiš.



Zobrazuji 2 komentáře:
Žák
Vůbec nechápu postup příkladu. Co je to cos?

Petr
cos je kosinus; jiste se to pocitat nejakou fintou typu rovnostranny trojuhelnik ma vsechny uhly 60 stupnu - cili aj jedna uhlopricka je u1=a=160 cm.  Dale z pytagorovy vety a z faktu ze se uhlopricky rozpoluji plati:

a2 = (u1/2)2+(u2/2)2
a2 = a2/4+u22/4
3a2 = u22
u2 = a * sqrt(3) = 160* sqrt(3) = 277.12

Ale pro jine uhly jako 60 stupnu jedine cez sin a cosinus!





Tipy na související online kalkulačky
Pythagorova věta je základ výpočtů kalkulačky pravouhlého trojuholníka.
Kosinovú větu přímo používá kalkulačka SUS trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.

K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:

Jednotky fyzikálních veličin:

Úroveň náročnosti úkolu:


 
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1   video2

Související a podobné příklady: